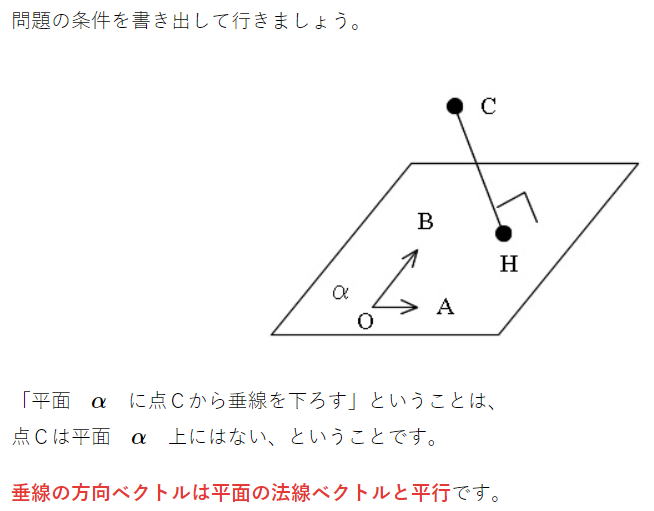
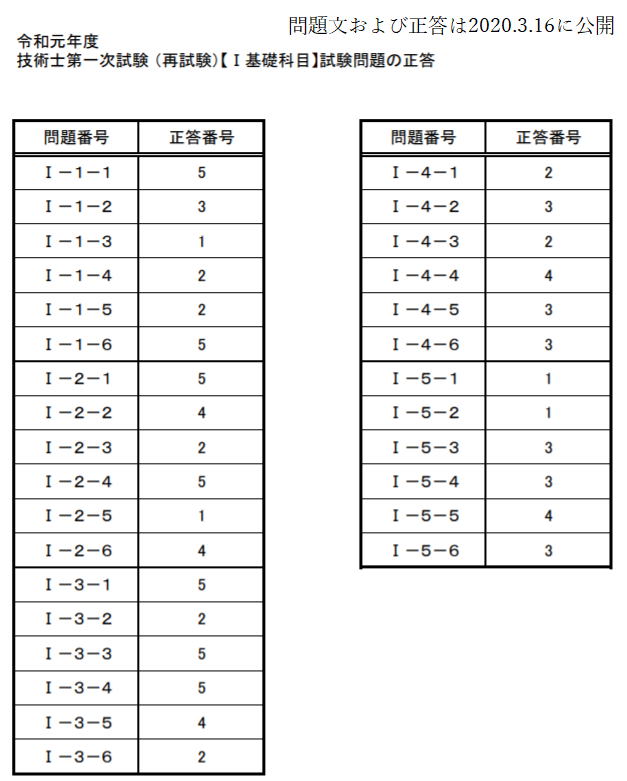
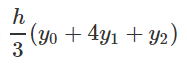| 令和元年度 技術士一次試験(再試験) 基礎科目 解答 10月13日に実施、10月21日に公開されたその試験問題の解答を作成する。 なお、問題文は著作権の関係もあり、必要に応じて最小限の引用にとどめる。 技術士一次試験の目次一覧に戻る 書籍 技術士一次試験 基礎科目を極める(2022年版) 平成16年度~令和3年度 基礎科目の解答を収録 基礎科目について、 過去の問題と今回の問題比較 類似の問題が多数ありますので、やはり過去問をしっかりとやるということに尽きます。 各群より3問選択 合計で15問解答 内8問正解で基礎科目は合格 なお、日本技術士会が現在公開している平成16年~28年の過去問356題の解答は 技術士一次試験・基礎科目 H16年~28年の356全問解答集 にまとめて記しています。 令和元年度技術士一次試験(再試験) 基礎科目 1群 Ⅰ-1-1 式で与えられる数値の大小比較 Ⅰ-1-2 線形計画問題の解法解説 Ⅰ-1-3 システムの信頼性を計算 Ⅰ-1-4 PERT法の理解度の確認 Ⅰ-1-5 製品製造時の期待損失額最小化 Ⅰ-1-6 設備・機械保全に関する知識確認 2群 Ⅰ-2-1 情報セキュリティ対策の知識確認 Ⅰ-2-2 ユークリッド互除法 Ⅰ-2-3 記憶装置の容量(テラバイト)を問う Ⅰ-2-4 計算機内での数の表記方法 Ⅰ-2-5 集合に関する理解を問う Ⅰ-2-6 直積集合から集合への写像の総数 3群 Ⅰ-3-1 3階微分とその係数 Ⅰ-3-2 定点から垂直に降ろされる平面上の点 Ⅰ-3-3 有限要素法の計算条件と精度 Ⅰ-3-4 シンプソンの1/3数値積分公式 Ⅰ-3-5 固有振動数と固有振動モード Ⅰ-3-6 平面上の楕円孔が受ける応力 4群 Ⅰ-4-1 化合物の極性 Ⅰ-4-2 化合物の酸の強さの比較 Ⅰ-4-3 熱力学関数の理解確認 Ⅰ-4-4 製品または材料を構成する主元素 Ⅰ-4-5 コドン(DNA)とアミノ酸の種類 Ⅰ-4-6 DNA組換え技術 5群 Ⅰ-5-1 気候変動に関する理解度確認 Ⅰ-5-2 廃棄物処理・リサイクルに関する法 Ⅰ-5-3 エネルギー別標準発熱量の比較 Ⅰ-5-4 再生可能エネルギーの比率 Ⅰ-5-5 科学史(年代順に並べる) Ⅰ-5-6 リスクコミュニケーション 技術士一次試験・基礎科目 H16年~28年の356全問解答集へ戻る R01年 基礎科目(再試験)問題 解答 1群 設計・計画に関するもの R01年 基礎科目(再試験)問題 トップに戻る Ⅰ-1-1 式で与えられる数値の大小比較 ボーナス問題 解答:⑤ 私なりの簡便法で解く。 1)a1=2、a2=2とすると左辺=2、右辺=2で「ア」の符号は「=」、a1=2、a2=8とすると左辺=4、右辺=5で「ア」の符号は「<」 従って、「ア」は「≦」である。 数学的解法(簡略)は2次で考える。 (a+b)2-4ab=(a-b)2である。 2)θ=π/4とすると左辺=2√2/πで「イ」は「>」、θπ/2とすると左辺=2/πで「イ」は「=」 従って、「イ」は「≧」である。 数学的な解法は、lim θ→+0 sin(θ)/θ=1を用いる。その後、0からπ/2までのsin(θ)とθのグラフを描く。 3)f(x)=x2とする。f''(x)=2>0 与えられた条件を満たしているf(x)である。 x1=1、x2=3とすると、左辺=((1+3)/2)2=4、右辺=(12+32)/2=5 従って、「ウ」は「<」である。 ※問題文にx1とx2は異なる2点と断りがある。x1=x2のときには左辺=右辺となる。 数学的な解法には、下に凸な二次曲線をイメージする。 Ⅰ-1-2 線形計画問題の解法解説 ボーナス問題 同じ問題がH18Ⅰ-1-2に、シンプレックス法を用いた解法がH28 Ⅰ-1-5にあります 解答:③ 解答は次のようになる。シンプレックス法という言葉はよく知られているが、その中身となるとこの方法を使いこなしていなければ理解の外である可能性が大きい。 以下に、シンプレックス法、双対問題、トレードオフ、パレート解が何であるかの理解を得るため、Webよりその説明部分を引用した。この引用部分を熟読の上で再度問題文に当たってもらいたい。  シンプレックス法(Wikipedia) シンプレックス法は、実行可能解 (超多面体の頂点) の1つから出発して目的関数の値をなるべく大きく (小さく) するようなところに移動させていく動作を繰り返して最適解を見つけ出す方法である。各ステップで必ず目的関数の値は改善される。 コンプレックス法 この用語はあるが、メジャーな用語ではないようだ。たとえば、「コ ンプ レックス法 に よる動 力学 を考慮 した マ ニ ピュレー タの障害物 回避 軌道生成」 双対問題(Wikipedia) 数学において、最適化問題における主問題(英: primary problem)の補問題を指す。どちらか一方の解法が両方の問題の解法となる。 逆問題(Wikipedia) 数学・物理学の一分野であり、入力(原因)から出力(結果、観測)を求める問題を順問題(じゅんもんだい、英: Direct problem)と呼び、その逆に出力から入力を推定する問題や入出力の関係性を推定する問題を逆問題と呼ぶ。 トレードオフ(Wikipedia) 何かを得ると、別の何かを失う、相容れない関係のことである。平たく言うと一得一失(いっとくいっしつ)である。対義語は両立性(コンパチビリティ、英: compatibility)。トレードオフのある状況では具体的な選択肢の長所と短所をすべて考慮した上で決定を行うことが求められる。 トレードオン トレードオフの逆と考えてよい。メジャーには使われていない。たとえば、「トレード・オン:経済・環境・社会の価値を同時に高める、これからのビジネス戦略」 パレート解(CAE用語辞典) パレート解とは、多目的最適化問題において、理想的な解にできるだけ近く、目的関数同士のバランスの異なる解のことです。複数のパレート解で構成される曲面をパレートフロンティアと呼びます。多目的最適化問題とは、改善したい目的関数が複数あり、なおかつそれらが互いに競合関係にある問題のことです。 たとえば、性能向上vs低コスト、軽量化vs剛性向上などは多目的最適化問題といえます。 アクティブ解 メジャーな用語ではないようです。 Ⅰ-1-3 システムの信頼性を計算 ボーナス問題 過去に多くの類似問題が出題されている 解答:①  Ⅰ-1-4 PERT法の理解度を確認 ボーナス問題 過去に多くの関連問題が出題されている。 最近でもH30 Ⅰ-1-2、H28 Ⅰ-1-4と頻出問題である。 解答:② (エ)これが誤りである。正しくは、クリティカルな作業(余裕のない作業)にかかる時間を縮めることにより、全作業にかかる全時間を短くすることができる。 過去問を自力で解いてみると、その仕組みが理解できる。 Ⅰ-1-5 製品製造時の期待損失額最小化 ボーナス問題 解答:② 条件に従って表を作成し、その合計が最小となる x を求める。最小値と断ってあるので、表からx=1.25である。x=1.75、x=2.00の計算は必要ない。 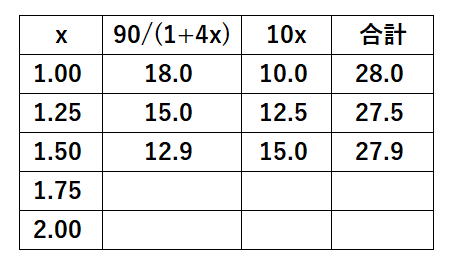 数学に自信がある人は、f(x)=90/(1+4x)+10xを微分し、f'(x)=0とすれば合計を最小とする x が求まる。 X=1+4xと置いて微分を進めると、一次微分f'(x)=-4×90/(1+4x)2+10、これをゼロと置くとx=1.25と求まる。 Ⅰ-1-6 設備・機械保全に関する知識確認 ボーナス問題 過去にH26 Ⅰ-1-5に出題がある 解答:⑤ 非常に基本的な、知識を問う問題です。過去問(H26 Ⅰ-1-5)によくまとまっていますので、確認してください。  2群 情報・論理に関するもの R01年 基礎科目(再試験)問題 トップに戻る Ⅰ-2-1 情報セキュリティ対策の知識確認 ボーナス問題 過去問のH22 Ⅰ-2-5、H20 Ⅰー2-5、H16 Ⅰー2-2が関連出題 直近ではH30 Ⅰ-2-2にも関連出題が 解答:⑤ 超ボーナス問題ですので、解説は省略いたします。 Ⅰ-2-2 ユークリッド互除法 ボーナス問題? 解答:④ ユークリッドの互除法(Wikipedia) 今持っている知識を駆使する。中学校で習った?方法で最大公約数は次に示すように3である。従って「ア」は3である。  次に問題文では複雑な説明が続いているが、ポイントは次の行列式が解けるかということである。これが解ければ x と y 、すなわち「イ」と「ウ」は求まる。 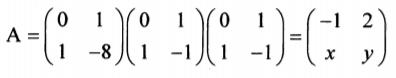 行列の掛け算の方法を示したが、これと同じ要領で行列の掛け算を進める。 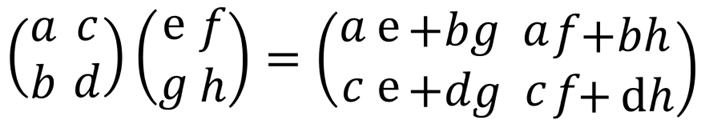 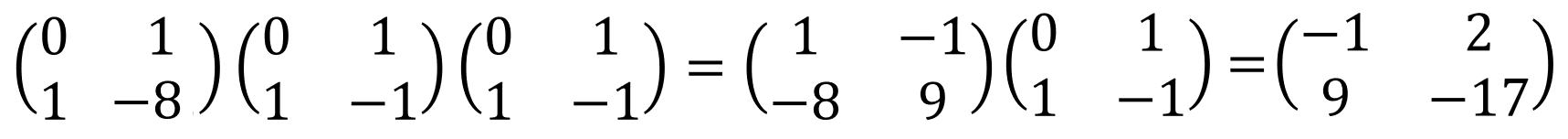 従って、x=9、y=-17となる。 Ⅰ-2-3 記憶装置の容量(テラバイト) ボーナス問題 解答:② この問題はひらめきが問われる。ひらめけば一瞬にして答えに至る。 文書D/文書Aで、単語1=21/7=3、同じく単語2=9/3=3、単語3=6/2=3 情報量が103倍となる度に、0.9765倍の乗率で情報量が変化する。これを表にすると次のようになるので、求める答えは1.8TBである。 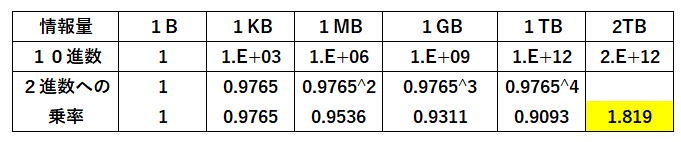 Ⅰ-2-4 計算機内での数の表記方法 関連問題がH29 Ⅰ-2-2で出題されている。 解答:⑤ 問題文に示されているように、ルールは4つである。  実数 13.0 をルール(1)に従って変形する。 13.0=23×(1+0.625) 符号部はプラスであるので、ルール(2)に従って、符号部分は 0 指数部は、α=3 であるから、ルール(3)に従って、3+127=130=(10000010)2 仮数部 0.625 は例題と同じであるから、10100000000000000000000 従って、答えは⑤である。 Ⅰ-2-5 集合に関する理解を問う ボーナス問題 同じ問題がH25 Ⅰ-2-4で出題されています。 類似の問題が、H30 Ⅰ-2-6およびH22 Ⅰ-2-3にあります。 解答:① 問題文に与えられているのは、図Aおよび図Bに関する情報である。 「情報」という語を含み、「論理」という語を含まない数は、65万-55万=10万となる。 これは図Dの赤線で囲った部分である。 さて、「論理」という語を含まない最大の数は図Cである。100万-55万=45万である。 最小の数は、図Dの赤線で囲んだ部分であり、10万である。 従って、答えは①となる。 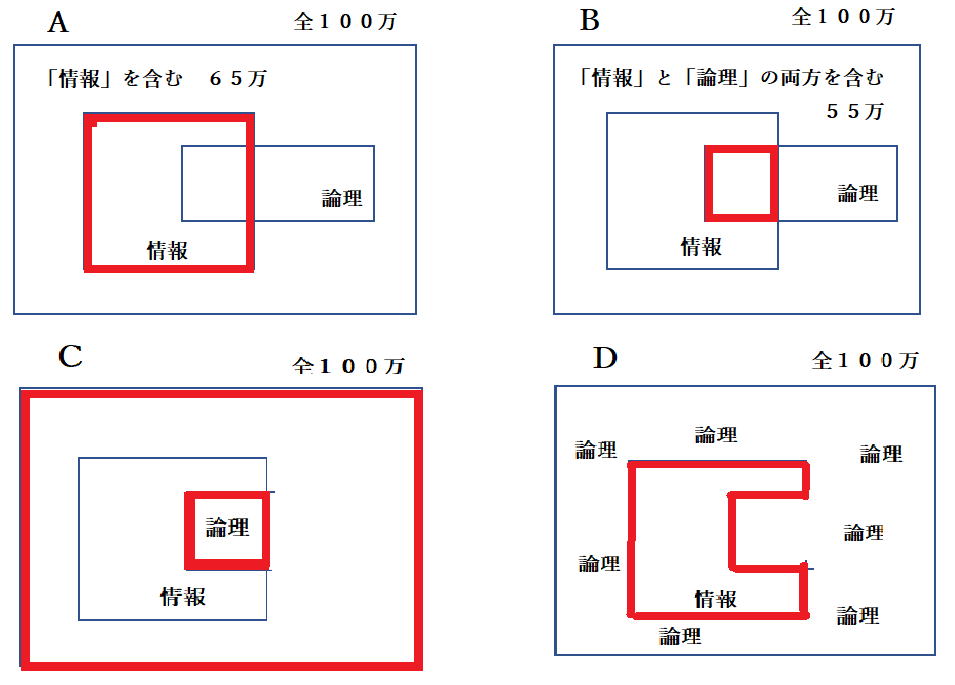 Ⅰ-2-6 直積集合から集合への写像の総数 見始めの問題です。 問題文です  解答:④ 直積集合 https://mathwords.net/tyokusekisyugou 集合 A と B の直積は、A×B という記号で表します。 例えば、A={1,2}、B={3,4,5}
のとき、 A×B={(1,3),(1,4),(1,5),(2,3),(2,4),(2,5)} となります。 A の要素と B の要素を1つずつ取ってきて作ったペアを全て集めた集合です。 また、A={1,2}、B={1,2,3}
のとき、 A×B={(1,1),(1,2),(1,3),(2,1),(2,2),(2,3)} となります。(1,2) と (2,1)
は別の要素であることに注意してください(順序が違えば別物とみなす)。 集合と写像 http://www.rimath.saitama-u.ac.jp/lab.jp/fsakai/set.html 2. 写像 集合 A の各元に対して,集合 B の元がただ1つ対応する規則 f が定まっているとき,この対応を A から B への写像といい,f: A → B で表す. まず直積集合 A×Bは A×B={(aα)(aβ)(bα)(bβ)(cα)(cβ)(dα)(dβ)}

最大応力は上式でx = a(楕円孔長辺縁)の位置で発生し、この点で応力集中係数は次のようになる。
あるいはx = aの点における曲率半径を用いて次のようにも表される。
楕円孔は、b → 0とすればき裂(グリフィスき裂)の問題となり、また、等価楕円の概念を利用して任意形状の切欠きの応力集中系数を近似できる場合があるなど、他の問題への応用の広がりが大きい。 4群 材料・化学・バイオに関するもの R01年 基礎科目(再試験)問題 トップに戻る Ⅰ-4-1 化合物の極性 ボーナス問題 H22 Ⅰ-4-1に類似問題 解答:② 図はWikipediaからである。異種の原子間、例えばC-O、C-H、B-F、C-Cl結合では、その結合に電子の偏りが生じ、極性が生まれる原因となる。ただし、二酸化炭素、メタン、三フッ化ホウ素、四塩化炭素では、図からもわかるように化合物の対称性がこの偏りを相殺し(極性ベクトルの重ね合わせがゼロとなり)、その結果として分子は無極性となる。ジエチルエーテルでは、このベクトルの重ね合わせでC-O結合の持つ極性を打ち消すことができないので、その結果、分子が極性を持つことになる。 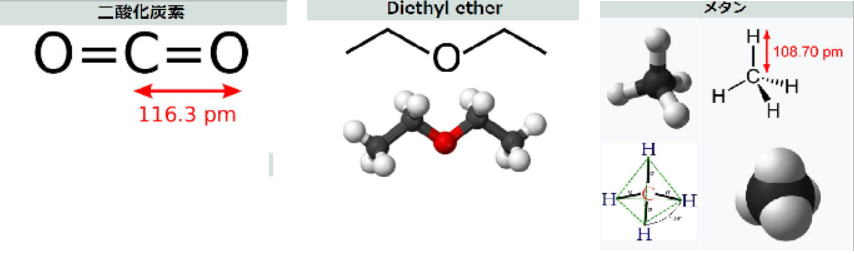 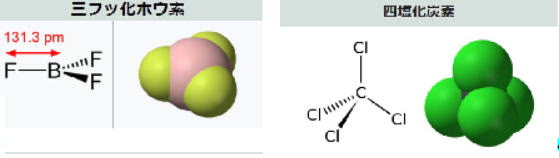 Ⅰ-4-2 化合物の酸の強さ ボーナス問題 H23 Ⅰ-4-2に出題あり そこより引用する 正解:③ H23年 Ⅰ-4-1 正答: ② (解答)
(参考) 酸解離定数(Wikipedia)より  Ⅰ-4-3 熱力学関数の理解確認 超ボーナス問題 正解:② 熱力学の基本公式 ΔG=ΔH-TΔS 教科書の一番最初に出てくる公式である。 Ⅰ-4-4 製品または材料を構成する主元素 H18 Ⅰ-4-3、H29 Ⅰ-4-4に関連問題 以下に引用数する。 解答:④ 以下の引用で記されていないのはリチウムイオン二次電池正極材である。 リチウムイオン二次電池(Wikipedia)  H18年 Ⅰ-4-3 引用 正答: ① (解答) 永久磁石(Wikipedia)より 永久磁石の原料として、3d遷移元素の鉄、コバルト、ニッケルが挙げられる。単体が室温で強磁性を示すのは、これら3つの元素のみである。さらにランタノイドのサマリウム、ネオジムも磁石の原料として挙げられる。単体では強磁性を示さないが、4f軌道に余ったスピンが存在するため、これらを原料とすることで強力な磁石が実現できる。なお、4f軌道電子はスピンと共に軌道運動も磁性に寄与している。 乾電池(Wikipedia)より (※実に多くの種類の乾電池が記載されています。その中のたった一例として空気亜鉛電池が示されていました)空気亜鉛電池 (1.4V) - 耳掛式及び耳穴式、眼鏡と一体化されている補聴器の電源として使われている。(※銅板と亜鉛板、電解液に硫酸水溶液を使うボルタ電池は乾電池とは言いませんのでここでは亜鉛を選択するしかありません) 光ファイバー(Wikipedia)より 光ファイバーはコア(core)と呼ばれる芯とその外側のクラッド(clad)[注 1]と呼ばれる部分、そしてそれらを覆う被覆の3重構造になっていて、クラッドよりもコアの屈折率を高くすることで、全反射や屈折により出来るだけ光を中心部のコアにだけ伝播させる構造になっている。コアとクラッドはともに光に対して透過率が非常に高い石英ガラスまたはプラスチックでできている[3][2]。(※石英ガラスはSiO2です) ジュラルミン(Wikipedia)より 合金を構成するアルミニウム以外の金属の割合は以下の通りである。
Ⅰ-4-5 コドン(DNA)とアミノ酸の種類 ボーナス問題 H28 Ⅰー4-5に同一問題 解答:③ H28年 Ⅰ-4-5 引用 正答: ① (解答) 64-20=44のコドンのほとんどは20種類のアミノ酸に振り分けられる。1種類のアミノ酸に対していくつものコドンが存在する。 たとえば下図の左上では、UUUでもUUCでもフェニルアラニンが、UUAでもUUGでもロイシンが生成してくる。 なお、DNA鎖とRNA鎖では構成塩基が少し違っている(T→U)。 DNA(wikipedia)より DNA はデオキシリボース(五炭糖)とリン酸、塩基 から構成される核酸である。塩基はプリン塩基であるアデニン(A)とグアニン(G)、ピリミジン塩基であるシトシン(C)とチミン(T)の四種類ある。 RNA(Wikipedia)より RNAの核酸塩基はアデニン (A)、グアニン (G)、シトシン (C)、ウラシル (U) の4種で構成されている。アデニン、グアニン、シトシンは DNA にも同じ構造が見られるが、RNAではチミン (T) がウラシルに置き換わっており、相補的な塩基はアデニンとなる。チミンとウラシルは共にピリミジン環を持つ非常に似た塩基である。 コドン(Wikipedia)より  Ⅰ-4-6 DNA組換え技術 H29 Ⅰ-4-6に類似問題 自信がなければ近寄らぬこと 解答:③ まず、類似問題をここに引用し、その後、補足説明を行う。 H29 Ⅰ-4-6より 正答は①  この問題は知識がなくては解答できない。自信がなければ避けて通るべき問題である。 設問① 正答であるので、この内容は正しい。 設問② 成功年が誤っています。 1979年には組換え医薬品第1号として、米国ジェネンテック社の研究者が世界で最初に大腸菌で生産させたヒト型インスリンが登場します。(バイオ技術で薬を作る) 設問③ 陰極に向かってではなく陽極に向かってです。 緩衝液などに核酸(DNA/RNA)を溶解すると、リン酸残基によりマイナスに荷電します。この溶液(DNA 試料) をアガロースゲルに添加し、緩衝液中で電気泳動を行なうと+側(陽極) に移動します。(アガロースゲル電気泳動) 同じ長さになるとは限らない。 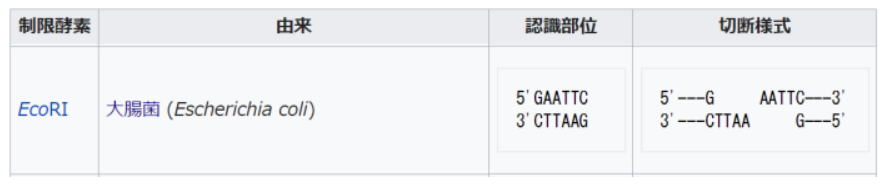 設問⑤ 「臓器や組織におけるDNAの偏在はない?」との設問です 受精すると、父親と母親から由来の遺伝子が交差して、新たな遺伝子が作り出される。この遺伝子が分化を繰り返し、一個体を作り上げる。最初の1つのDNAがコピーを繰り返して一個体を作り上げるため、体のどの部分をとっても最初のDNAと全く同じDNAが存在していることになる。ただし、そのDNAから器官(肝臓など)が作られるときにはそれに必要な遺伝子機能のみが活性化し、不要な部分は不活性とされる。(興味ある方はiPS細胞も参考としてください) 下の図から、ゲノムライブラリーはDNA全体から切り出された部分であり、cDNAライブラリーは器官の発現に利用されたDNA部分に由来していることが分かる。従って、この設問の内容は誤りである。 なお、cDNAとは相補的DNAのことである。 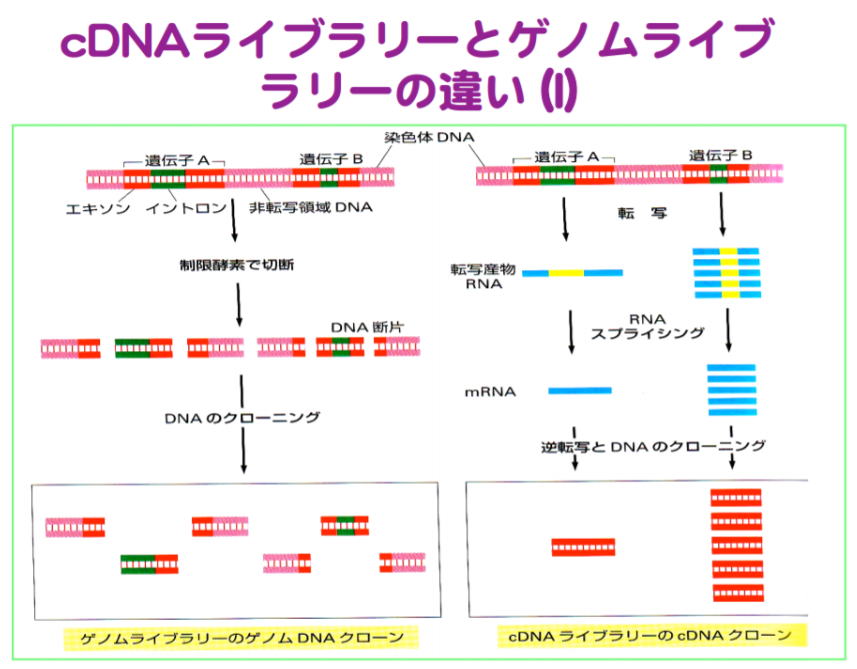 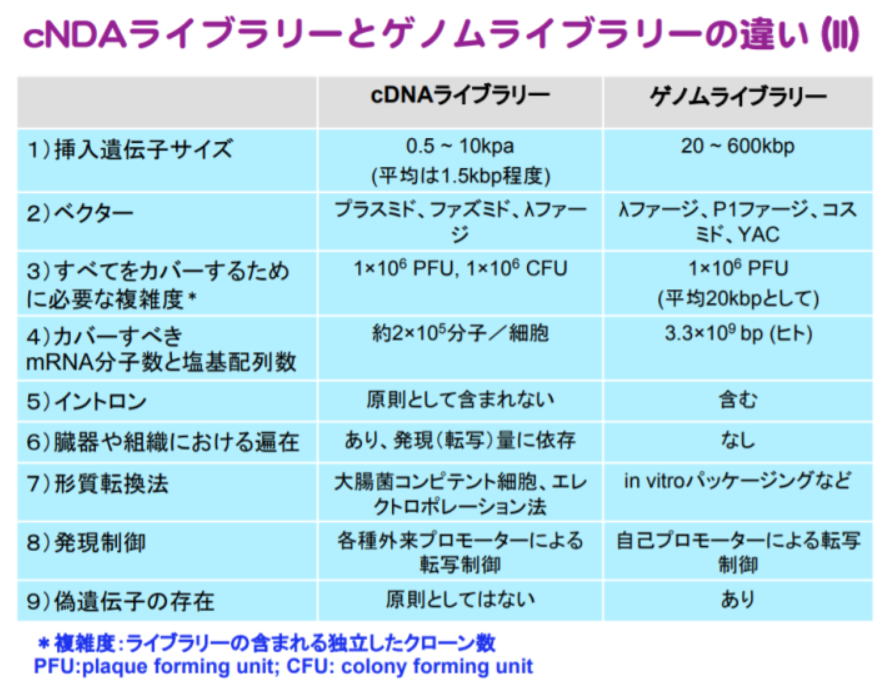 今回の問題の解説 今回の問題  解説 ①誤り 1979年。上記②の解説を参照のこと。 ②誤り 倍々と増えていくので、30回の反復増幅により230倍に複製される。ポリメラーゼ連鎖反応(Wikipedia)を参照のこと。 ③正しい 上記⑤の解説を参照のこと。 ④誤り 上記④の解説を参照のこと。 ⑤誤り 陽極に向かって移動し 上記③の解説を参照のこと。 5群 環境・エネルギー・技術に関するもの R01年 基礎科目(再試験)問題 トップに戻る Ⅰ-5-1 気候変動に関する理解度確認 ボーナス問題 関連問題はR01 Ⅰ-5-2 持続可能な開発目標(SDGs) H30 Ⅰ-5-1も重要です。 解答:①  この文章は、白書の「はじめに」より引用されたものです。 Ⅰ-5-2 廃棄物処理・リサイクルに関する法 H24 Ⅰ-5-1に出題あり。 解答:① H24 Ⅰ-5-1を再記する。 正答: ③ (解答) 法文を深く読み込まないと、解答には至りません。自信がなければパスとする問題です。 「循環型社会形成推進基本法は、焼却するごみの量を減らすことを目的に、リサイクルを最優先とする社会の構築を目指した法律である。」は誤り。 3R(Reduce、Reuse、Recycle)の順です。 「容器包装リサイクル法(容器包装に係る分別収集及び再商品化の促進等に関する法律)では、PETボトル、スチール缶、アルミ缶の3品目のみについて、リサイクル(分別収集及び再商品化)のためのすべての費用を、商品を販売した事業者が負担することを義務付けている。」は誤り。 家電リサイクル法(特定家庭用機器再商品化法)では、エアコン、テレビ、洗濯機、冷蔵庫など一般家庭や事務所から排出された家電製品について、小売業者に消費者からの引取り及び引き取った廃家電の製造者等への引渡しを義務付けている。 「家電リサイクル法(特定家庭用機器再商品化法)では、電子レンジや冷蔵庫などの主な家電製品について、リサイクルのための費用を製品の購入時にあらかじめ消費者が負担することが義務付けられている。」は誤り。 電子レンジは含まれていない。消費者が廃棄時にリサイクルのための費用を負担する。 対象となる容器包装は、ガラスびん、PETボトル、紙製容器包装、プラスチック製容器包装、アルミ缶、スチール缶、紙パック、段ボールです. 「建設リサイクル法(建設工事に係る資材の再資源化等に関する法律)では、特定建設資材を用いた建築物等に係る解体工事又はその施工に特定建設資材を使用する新築工事等の建設工事のすべてについて、その発注者に対し、分別解体等及び再資源化等を行うことを義務付けている。」は誤り。 (建設工事の規模に関する基準) 面積、金額に関する規定がある。 「バーゼル条約(有害廃棄物の国境を越える移動及びその処分の規制に関するパーゼル条約)は、発展途上国から先進国へ有害廃棄物が輸入され、環境汚染を引き起こした事件を契機に採択されたものであるが、リサイクルが目的であれば、日本から発展途上国に有害廃棄物を輸出することは規制されてはいない。」は誤り。 輸出国と輸入国、双方の許可が必要となります。 この過去問のページには、各法令についての解説も添付しています。 Ⅰ-5-3 エネルギー別標準発熱量の比較 解答:③ 資源エネルギー庁エネルギー源別標準発熱量表を参照となっています。 このような表もありますが、重量と体積間の換算が必要となります。 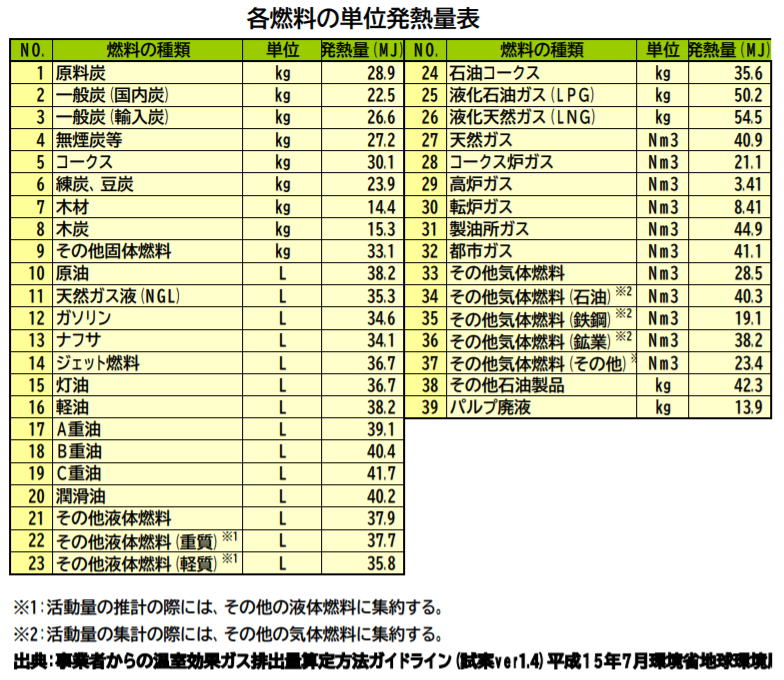 この問題を解くには、持っている常識に頼ります。すなわち、重量当たりの水素含量の大きな燃料は発熱量が大きい、次いで炭素含量の大きな燃料が発熱が大きい。 LNG(Liquid Natural Gas)はCH4で水素が多く含まれています。原油(石油)はCHX(一般的にはCmHnと表わす))でこのXは4より小さな値です。石炭はCです。 木材はCm(H2O)nですので、発熱量は石炭に劣ります。こう考えていくと、自然に解答に至ります。ポイントはLNGの主成分がメタン(CH4)であることを知っていたか、ということです。 Ⅰ-5-4 再生可能エネルギーの比率 解答:③ わが国の一次エネルギー供給量に占める再生可能エネルギーの比率は、Webで簡単に見つけられそうであるが、これが案外難しい。緊急避難的に2015年のデータをWikipediaより得た。水力と地熱・風力・太陽光・バイオマス等の合計で9.4%である。2017年度はこれよりも再生可能エネルギーの利用が進んできているとして、③11%がその答えになる。 日本のエネルギー資源(Wikipedia) 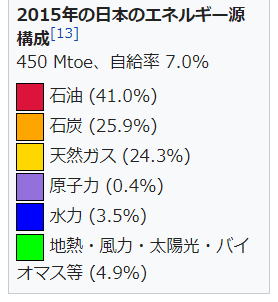 Ⅰ-5-5 科学史(年代順に並べる) 解答:④ (ア)ワット式蒸気機関の発明 1776年 (イ)進化の自然発生説 1859年 (ウ)フロンティア軌道理論 1952年 (エ)周期彗星の発見 1682年頃 (オ)一般相対性理論の発表 1915~16年 従って、答えは④である。 Ⅰ-5-6 リスクコミュニケ―ション 解答:③ 常識的に判断すると、答③に至ると思います。下に引用したリスクコミュニケーションからも、関係者間で情報を共有し、情報を正しく理解し、意思疎通を図っていく、そのためのコミュニケーションであることが分かります。このコミュニケーションを行わない場合には、個々それぞれが独自の捉え方をしている可能性があるということです。 リスク評価(リスク管理Navi)より リスク・コミュニケーション(Wikipedia) リスクコミュニケーション (Risk Communication) とは社会を取り巻くリスクに関する正確な情報を、行政、専門家、企業、市民などのステークホルダーである関係主体間で共有し、相互に意思疎通を図ることをいう。合意形成のひとつ。 リスクコミュニケーションが必要とされる場面とは、主に災害や環境問題、原子力施設に対する住民理解の醸成などといった一定のリスクが伴い、なおかつ関係者間での意識共有が必要とされる問題につき、安全対策に対する認識や協力関係の共有を図ることが必要とされる場合である。 レギュラトリーサイエンスとは(日本薬学会) レギュラトリーサイエンスとは我々の身の回りの物質や現象について、その成因や機構、量的と質的な実態、および有効性や有害性の影響をより的確に知るための方法を編み出し、その成果を用いてそれぞれの有効性と安全性を予測・評価し、行政を通じて国民の健康に資する科学です。 (日本技術士会より公開された正答)
|