| 令和2年度 技術士一次試験 基礎科目 解答 10月11日に実施、10月19日に公開されたその試験問題の解答を作成した。(10月20日公開) 技術士一次試験の目次一覧に戻る 書籍 技術士一次試験 基礎科目を極める(2022年版) 平成16年度~令和3年度 基礎科目の解答を収録
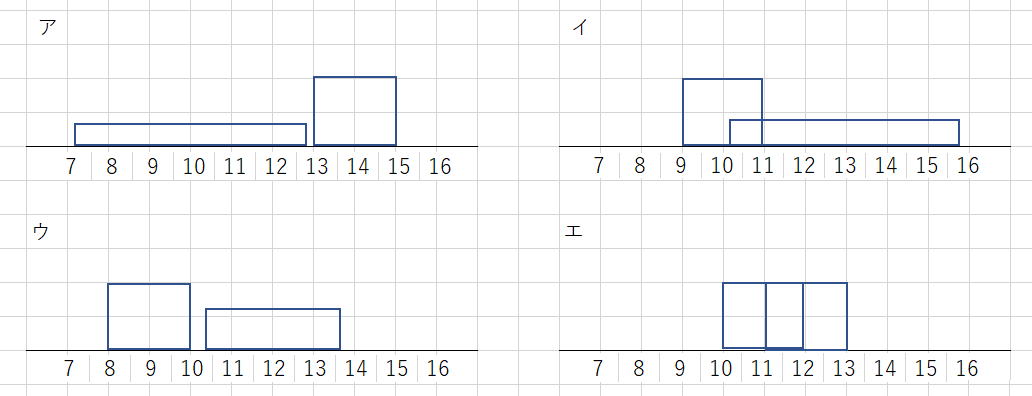
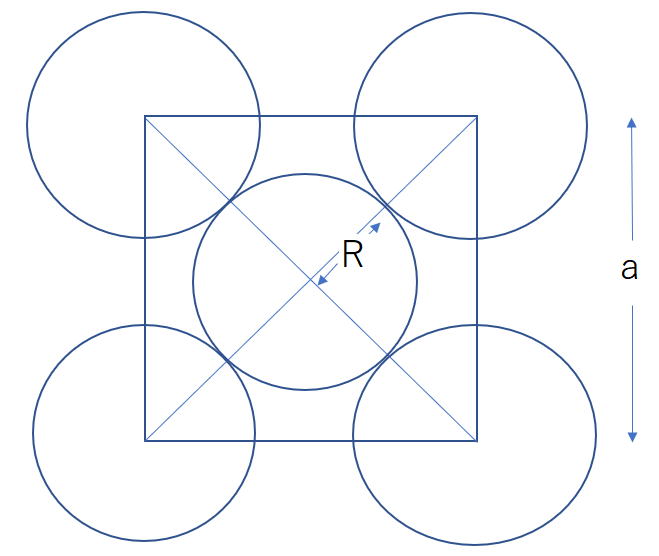
令和2年度技術士一次試験 基礎科目 1群 設計・計画 Ⅰ-1-1 ユニバーサルデザイン Ⅰ-1-2 材料の強度と応力 Ⅰ-1-3 応力による材料の変形 Ⅰ-1-4 生産量の最適化 Ⅰ-1-5 製図法におけるルール Ⅰ-1-6 システムの信頼度 2群 情報・論理 Ⅰ-2-1 情報の圧縮方法 Ⅰ-2-2 真理値表に基づく論理計算 Ⅰ-2-3 標的型攻撃への有効な対策 Ⅰ-2-4 2進数の補数表現 Ⅰ-2-5 2進を10進に変換するアルゴリズム Ⅰ-2-6 メモリ検索にかかる時間 3群 解析 Ⅰ-3-1 ベクトルの発散値を求める Ⅰ-3-2 関数のある点での傾きを求める Ⅰ-3-3 数値解析の誤差 Ⅰ-3-4 有限要素法の面積座標 Ⅰ-3-5 ばねの固有振動数 Ⅰ-3-6 配管中の水の流速計算 4群 材料・化学・バイオ Ⅰ-4-1 有機化合物燃焼時のCO2発生量 Ⅰ-4-2 有機化学反応の種類 Ⅰ-4-3 金属の性質比較 Ⅰ-4-4 アルミニウムの結晶構造 Ⅰ-4-5 酵母菌によるグルコース発酵 Ⅰ-4-6 PCR技術の特徴とその手順 5群 環境・エネルギー・技術 Ⅰ-5-1 プラスチックごみ問題 Ⅰ-5-2 生物多様性の保全 Ⅰ-5-3 日本のエネルギー消費 Ⅰ-5-4 日本のエネルギー情勢 Ⅰ-5-5 日本の産業技術発展の歴史 Ⅰ-5-6 科学技術史 技術士一次試験・基礎科目 H16年~28年の356全問解答集へ戻る R02年 基礎科目問題(日本技術士会) 解答 1群 設計・計画に関するもの R02年 基礎科目問題(日本技術士会) トップに戻る Ⅰ-1-1 ユニバーサルデザイン 解答:③ ノーマライゼーションは1950年代に北欧諸国から始まった社会福祉をめぐる社会理念のひとつで、障碍者も健常者と同様の生活ができるように支援すべきという考え方である。カスタマイズからは障碍者が健常者とは異なる環境で生活できるようにする、とのニュアンスが伝わってくる。 「基礎科目問題を極める」 pp29~30より ユニバーサルデザインは、ロナルド・メイスにより提唱されました。 特別な改造や特殊な設計をせずに、すべての人が可能な限り最大限まで利用できるように配慮された製品や環境設計をいいます。 (1)誰でも公平に利用できる(誰にとっても利用しやすくする) (3)単純で直感的に利用することができる (4)認知できる情報(必要な情報がすぐに理解できる) (5)失敗に対する寛大さ(失敗しても危険性がない) (6)少ない身体的な努力 (7)接近や利用のためのサイズと空間 Ⅰ-1-2 材料の強度と応力 解答:④ 「基礎科目問題を極める」 pp74~75に関連する問題(H29-1-1-6)があります。 この問題では、構造物の耐力Rと作用荷重Sが共に正規化された長方形で与えられ、RとSの重なり部分を破壊確率として算出しました。 本問題も基本的にはH29年度の問題と同じであると考えられますが、RおよびSが正規分布として与えられるところに違いがあります。厳密には正規分布を関数fR(x)、関数fS(x)として、重なり積分∫FR(x)fS(x)dxを求めなければなりませんが、短い試験時間内ではそのようなことは不可能に近いと考えられます。 そこで、簡易的にではありますが、問題文に与えられているμおよびσを反映させて、長方形にはなってしまうのですが、イメージが沸くように図を作成しました。(ア)~(エ)のいずれも、図の左側が材料に生じる応力S、右側が材料の強度Rです。
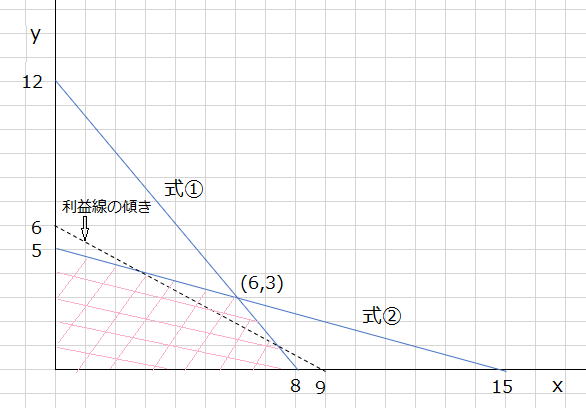
問題文では「Z=R-Sが0を下回る確率Pr(Z<0)が一定値以下となるように設計する」と記されています。(Z<0)は紛らわしい表現ですが、Zが負になると材料の破壊が起こるという意味です。したがって、この破壊の起こる確率Prが小さなケースはどれですか? とこの問題は聞いています。 いま仮に、SとRが大きく離れている場合は、応力Sに対して非常に頑丈な材料であり、Z=R-S(正規分布の重なりPr)は非常に小さな値となります。SとRが大きく重なった時には材料の破壊確率Prは大きくなり、SとRの位置関係が図で示したものと逆転したときには、材料の破壊される確率Prはきわめて大きな値となります。 この図からは、一番材料が破壊される可能性が大きいのが、RとSが大きく交わっている(エ)、次に大きいのが(イ)であることがわかります。 (ア)と(ウ)の重なり(面積)は正規分布曲線を考えたとき、どちらが大きいか悩ましいところがありますが、(ア)の背の低い長方形で示したほうが、正規分布として評価したときには遠くまでそのすそ野をのばし、さらに図で示した四角形同士がより接近していますので、その結果重なり積分における重なりの面積がより大きくなると推定されます。 さらにこの問題で重要なことは、(ア)においては、左に示した長方形Sを正規分布としてイメージしたとき、そのすそ野の広がりは右の正方形Rを超えてさらに右方向までそのすそ野を伸ばしています。このすそ野の部分では、S>Rとなり材料の破壊が起こることになり、その結果として構造物が破壊される確率Prは高くなります。同じことを(ウ)でも確認してください。(ア)との歴然とした違いが見えてきます。 材料が破壊される確率Prは(ア)>(ウ)となります。 したがって、破壊のされやすさは、(エ)>(イ)>(ア)>(ウ)の順となります。求められているのは材料が破壊されにくい順番、Pr(Z<0)の小さな順にですので、この逆順である④が答となります。 ※ 実に複雑ですね。もっと簡単な解法があります。それなら4分以内に答に至ります。 (参考) 講座 Lecture 機械・構造物の信頼設計 5.故障物理と信頼性理論 中川隆夫、福田収一 「材料」 第31巻 第347号 pp840~846 からの一部抜粋 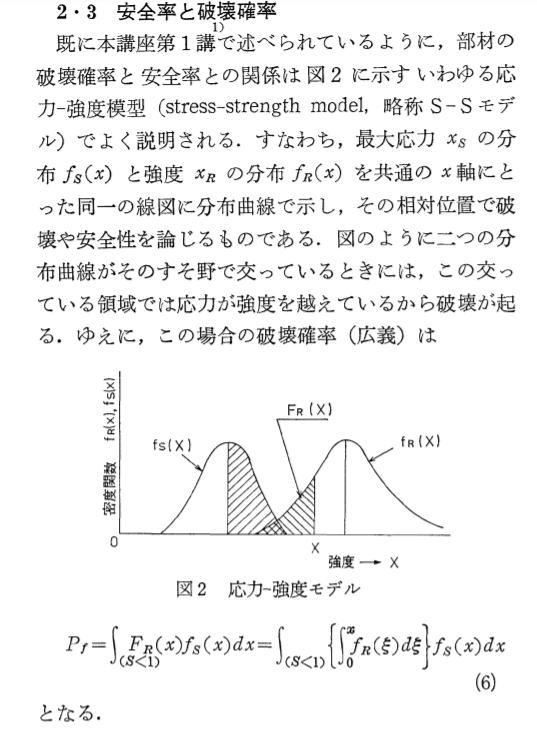 Ⅰ-1-3 応力による材料の変形 解答:③ (ア)誤り 弾性とは、外力によって変形した物体が、その外力が取り除かれたときに元の形に戻ろうとする性質です。 したがって、変形してしまっては弾性とは言いませんので誤りです。 (イ)誤り 固有振動数と破断は関係のない話です。 (ウ)正しい 座屈に関しては「基礎科目問題を極める」 pp68~69。 (エ)正しい (オ)正しい Ⅰ-1-4 生産量の最適化 解答:⑤ 「基礎科目問題を極める」 pp49~50が本問題を解く参考となる。 (1) 製品1の数をx個、製品2の数をy個とすると、使用できる原料AとBの重さに上限があるので、 3x+2y≦24 式① x+3y≦15 式② 一方、利益は 利益 z=2x+3y であるから、この利益線の一例をグラフ中に書き込むと、点線のようになる。この利益線はこの傾きを保ったまま上下に平行に動くので、利益が最大となる点は図中の(x、y)=(6,3)の点である。即ち、利益=2×6+3×3=21(百万円)が最大となる。 (2) (x、y)=(6,3)の点を維持するためのΔcを求める。 題意より、Δcを加味した利益線の傾きは、 -(2+Δc)/3 この傾きが式①の傾きと同じになるときには、Δc=2.5、式②の傾きと同じになるときの傾きは、Δc=-1となる。 (1)で決定した製品1、2の生産量は変わらないとしているので。x1=6、x2=3である。 したがって、本問題の答えは⑤である。
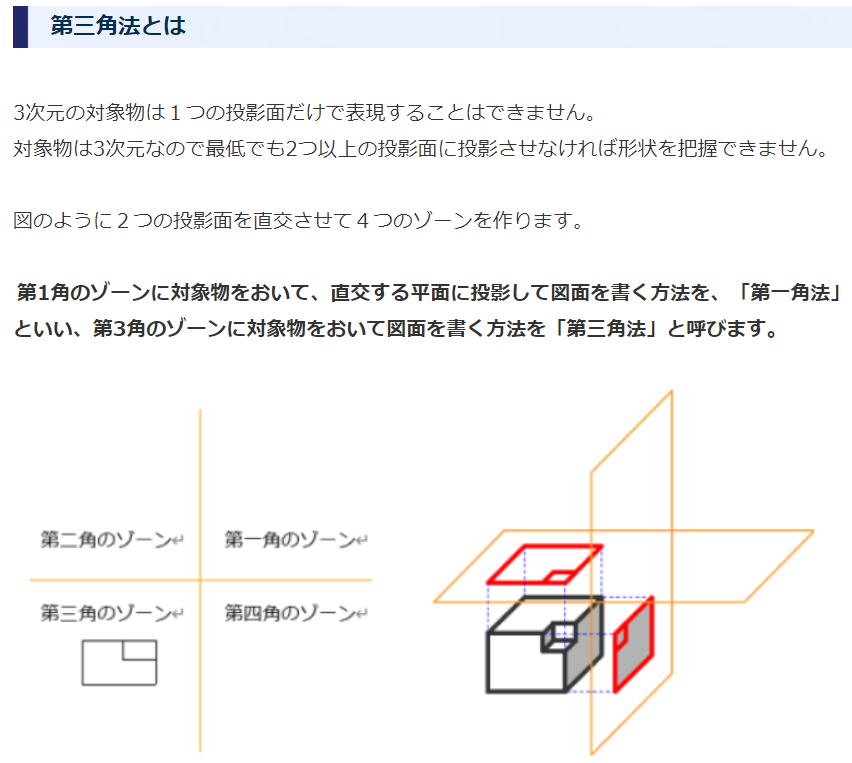
Ⅰ-1-5 製図法におけるルール 解答:⑤ まずは三角法の予備知識から。 図面の投影法(第三角法) 機械設計エンジニアの基礎知識 より
(ア)正しい (イ)誤り 左側面図は正面図の左に (ウ)誤り 細い破線または太い破線を、対象物の見えない部分の形状を表すのに用いる。 (参考)図面の描き方・見方(基礎) 「このような図が想像図である」は誤り。想像図という用語が見当たらない。 「このような線が想像線である」ならもっともらしく感じられるが、想像線の意味合いが違う。 (参考)想像線(JIS規格) (エ)誤り 投影法は明記する必要がある 図面は採用した投影法がわかるようにマークを記載するルールとなっています。 (参考)図面の描き方・見方(基礎) (オ)正しい Ⅰ-1-6 システムの信頼度 解答:③ 「基礎科目問題を極める」 p7参照 次の不等式を満足するnを求める。 (1-(1-0.7)n)×0.95≧0.94 n=4以上で、本不等式が成立するので、答えは③のn=4である。 2群 情報・論理に関するもの R02年 基礎科目問題(日本技術士会) トップに戻る Ⅰ-2-1 情報の圧縮方法 解答:④ ①と②は対となっていますので、ともに正しいかともに間違っているかです。不適切なものは1つのみですので、①と②は正しいことになります。 ③のJPEGとMPEGはWikipediaより抜粋、 JPEG(ジェイペグ、Joint Photographic Experts Group)は、コンピュータなどで扱われる静止画像のデジタルデータを圧縮する方式のひとつ。 一般的に非可逆圧縮の画像フォーマットとして知られている。 デジタルカメラの記録方式としてもよく利用されている。
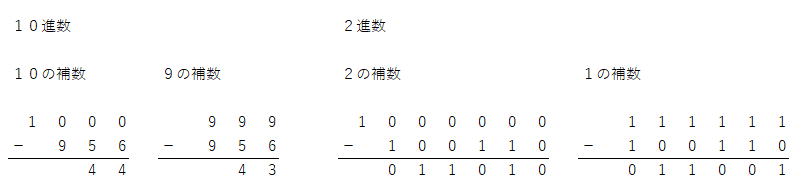
Ⅰ-2-5 2進を10進に変換するアルゴリズム 解答:⑤ 2進数を10進数に変換するアルゴリズムです。 変換すべき2進数は(11010101)2です。8桁数字で、a7=1,a6=1、a5=0、a4=1、a3=0、a2=1、a1=0、a0=1です。 開始から始まり、s←anは、まずはs←a7で、a7の持っている値1をレジストsに入れます。この←の意味が分かればこのアルゴリズムを追っかけていけます。 詳細は、各自で追っかけていただくとして、
したがって、答えは⑤となります。 アルゴリズムの問題は頻度高く出題されます。何通りかのアルゴリズムを実際に数値をあてはめながら自分で追いかけてみれば、自信が付くことと思います。 「基礎問題を極める」 pp136~146にアルゴリズム問題及びその解説があります。 Ⅰ-2-6 メモリ検索にかかる時間 解答:⑤ 「基礎科目問題を極める」 p94と同じ問題です。 50×0.9+450×0.1=90ns 3群 解析に関するもの R02年 基礎科目問題(日本技術士会) トップに戻る Ⅰ-3-1 ベクトルの発散値を求める 解答:② 「基礎問題を極める」 p198~201に同じです。 Vx=x、Vy=x2y+yz2、Vz=z3。 x=1、y=3、z=2です。 divV=∂Vx/∂x+∂Vy/∂y+∂Vz/∂z =1+x2+z2+3z2 =1+1+4+12 =18 Ⅰ-3-2 関数のある点での傾きを求める 解答:④ これも解き方は前問と同様ですね。
①~⑤のすべての化合物についてこの計算を実施してもよいのですが、要は炭素含有量の大きな化合物が単位重さ当たり多くの二酸化炭素を発生することに気が付けば、答を簡単に求めることができます。次の大小比較を下に示した燃焼の化学式と見比べることにより理解を深めてください。
炭素含有量の大小比較 CH4>CH3OH(CH4O)、C2H6>C2H5OH(C2H6O) C2H4>C2H6
C2H4>CH4(C2H4は2×CH2、CH2>CH4)
① CH4 + 2O2 → CO2 + 2H2O ② C2H4 + 3O2 → 2CO2 + 2H2O ③ C2H6 + 3.5O2 → 2CO2 + 3H2O ④ CH3OH + 1.5O2 → CO2 + 2H2O ⑤ C2H5OH + 3O2 → 2CO2 + 3H2O
Ⅰ-4-5 酵母菌によるグルコース発酵 解答:③ 「基礎科目問題を極める」 p292が理解できていれば容易に解ける。 題意に従って、化学式の係数を書き換える。 好気呼吸(与えられた式×1/3) 1/3C6H12O6+2O2+2H2O→2CO2+4H2O エタノール発酵(与えられた式×2) 2C6H12O6→4C2H5OH+4CO2 両式を足し合わせると、2モルの酸素を消費して6モルの二酸化炭素を発生していることがわかる。したがって、答えは③。 Ⅰ-4-6 PCR技術の特徴とその手順 解答:④ 「基礎科目問題を極める」 p280 にPCR(ポリメラーゼ連鎖反応)に関連する設問あり。 「ポリメラーゼ連鎖反応(PCR)では、一連の反応を繰り返すたびに二本鎖DNAを熱によって変性させなければならないので、熱に安定なDNAポリメラーゼを利用する」 本年度のこの問題の設問も「④耐熱性の高いDNAポリメラーゼが、PCR法に適している」で最も適切なものである。 ポリメラーゼ連鎖反応(Wikipedia)より引用する。 PCR法は、試薬を混交したDNA溶液の温度を上げて下げる、という一連の熱サイクルによって動作する。このDNAサンプルの加熱と冷却の繰り返しサイクルの中で、二本鎖DNAの乖離、プライマーの結合、酵素反応によるDNA合成、という3つの反応が進み、最終的に特定領域のDNA断片が大量に複製される。 PCR法では、増幅対象(テンプレート)のDNAサンプルの他に、大量のプライマー(標的DNA領域に相補的な配列を持つ短い一本鎖DNA(オリゴヌクレオチド))とDNAの構成要素である遊離ヌクレオチド、そしてポリメラーゼの一種であるDNA合成酵素(DNAポリメラーゼ)という3つの試薬を使用する。
以上のようにPCR法は、DNA鎖長による変性とアニーリングの進行速度の違いを利用して、反応溶液の温度の上下を繰り返すだけでDNA合成を繰り返し、任意のDNAの部分領域を増幅する技術である。 使用するDNAポリメラーゼが熱に弱い場合、変性ステップの高温下でDNAとともにポリメラーゼも変性してしまい、失活してしまう。そのためPCR法の開発当初は、DNA変性時の毎回にDNAポリメラーゼを酵素として追加しており、手間と費用がかかっていた[8]。現在では、サーマスアクアティカスという好熱菌由来の熱安定性DNAポリメラーゼであるTaqポリメラーゼなどを用いることで、途中で酵素の追加をせずに反応を連続して進めることができる。 PCRサイクル
①誤り 2本鎖DNAの水素結合を切断して ②誤り 温度をあげすぎると1本鎖DNAに対してプライマーが結合しにくくなる。 (参考)PCRによる診断のためのプライマー情報 ③誤り 増幅したいDNA配列が長くなるにつれて伸長反応時間は長くなる。 ④正しい ⑤誤り プライマーの塩基配列は当然含まれる。 5群 環境・エネルギー・技術に関するもの R02年 基礎科目問題(日本技術士会) トップに戻る Ⅰ-5-1 プラスチックごみ問題 解答:② (ア)正しい マイクロプラスチック(Wikipedia) マイクロプラスチック(英: microplastics)は、(生物物理学的)環境中に存在する微小なプラスチック粒子であり、特に海洋環境において極めて大きな問題になっている[1]。一部の海洋研究者は1 mmよりも小さい顕微鏡サイズの全てのプラスチック粒子[2]と定義しているが、現場での採取に一般に使用されるニューストンネットのメッシュサイズが333 μm (0.333 mm) であることを認識していながら[3]、5 mmよりも小さい粒子と定義している研究者もいる[4][5]。 日本の環境省はサイズが5mm以下の微細なプラスチックごみと定義している。 (イ)誤り プラスチックを取り巻く国内外の状況 環境省(平成30年8月)
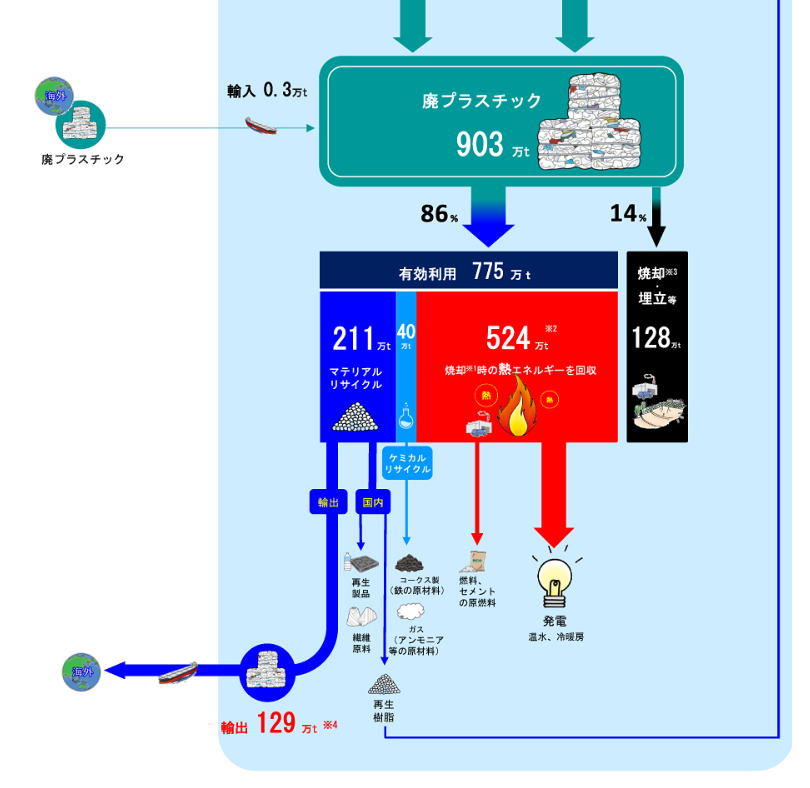
(ウ)誤り 問題文のどこが間違いであるかを検証していきましょう。 中国が廃プラスチック等の輸入禁止措置を行う直前の2017年 これは正しいです。 中国 2017年7月 「輸入廃棄物管理目録」を改正 2018年1月より生活由来の廃プラスチックや未分別の紙くずや繊維くずなどの資源ごみが中国へ輸出できなくなった。 2017年に日本国内で約900万トンの廃プラスチックが排出され これも正しいです(下図参照) そのうち約250万トンがリサイクルされている これも正しいです(下図参照) マテリアルリサイクル211万トン+ケミカルリサイクル40万トン=251万トンのリサイクル 海外に輸出され海外でリサイクルされたものは250万トンの半数以下であった 誤りがあるとするとこの部分(下図参照) 輸出129万トンはリサイクル251万トンの51.4%>50% 輸出されたものすべてが海外でリサイクルされたとは限らない。 これが誤りであるとの判断はなかなかに難しいと思います。 解答の選択肢①~⑤において、(ア)が正しく、(イ)が誤りであるとするものは②のみですから、(ウ)の正誤判定ができなくても正解に至ることはできそうです。 プラスチックの天然資源採掘、生産、リサイクル、廃棄の流れ(2017年推計値) このサイトには、生産から廃棄、そしてリサイクルまでの一連の流れが記されています。その中より、今の問題に関連がある部分を抜き出しました。
(エ)正しい 「プラスチック資源循環戦略」の策定について(環境省、2019年5月31日) (オ)正しい 海洋プラスチック問題について(WWF、2018年10月26日) 問題になっている海洋プラスチックの8割以上は、陸上で発生し海に流入したもの。特に多いのが、使い捨て用が中心の「容器包装用等」。この用途に使われるプラスチックは、世界全体のプラスチック生産量の36%、世界で発生するプラスチックごみの47%を占めていると考えられます。 Ⅰ-5-2 生物多様性の保全 解答:③ ③誤り 「基礎科目問題を極める」 pp348~349(H28-1-5-2に同じ) 移入種問題は、生物多様性の保全上、最も重要な課題の1つとされているが、我が国では移入種の駆除の対策は禁止されていない。
日本在来の生物を捕食したり、これらと競合したりして、生態系を損ねたり、人の生命・身体、農林水産業に被害を与えたりする、あるいはそうするおそれのある外来生物による被害を防止するために、それらを「特定外来生物」等として指定し、その飼養、栽培、保管、運搬、輸入等について規制を行うとともに、必要に応じて国や自治体が野外等の外来生物の防除を行うことを定める。
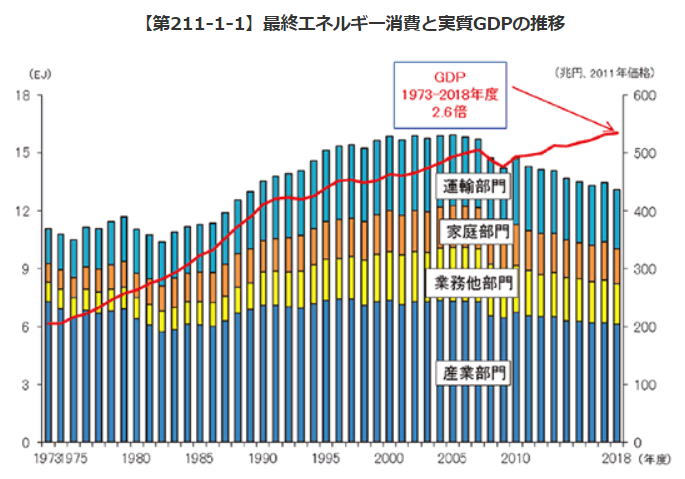
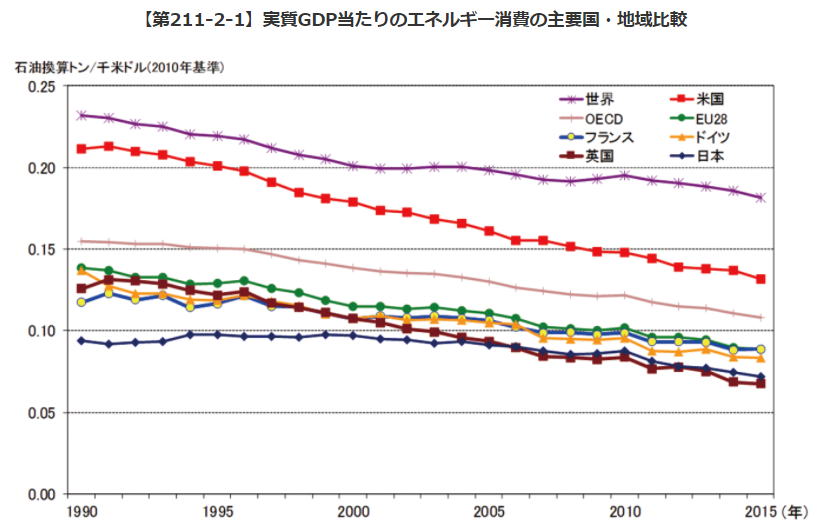
②正しい 上図参照 ③正しい エネルギー白書2020 より
④誤り ①で示した図を参照 ⑤正しい 常識的に判断 Ⅰ-5-4 日本のエネルギー情勢 解答:① 「基礎科目問題を極める」 pp311~312(H24-1-5-3に同じ) 解答を問題文にはめ込み、内容を確認ください。 Ⅰ-5-5 日本の産業技術発展の歴史 解答:④ ④誤り 統計的品質管理法が我が国に取り入れられたのは第二次世界大戦後です。 科学的管理法(Wikipedia) より テイラーの主張した科学的管理法の原理は、 統計的品質管理の歴史
物理 1608年 ガリレイ 天体望遠鏡で天体観測 物理 1656年 ホイヘンス 振り子時計を発明 物理 1705年 ハレー 周期彗星の発見 物理 1712年 ニューコメン 大気圧機関の発明 電気 1752年 フランクリン 雷の電気的性質の解明 物理 1771年 アークライト 水力紡績機を発明 物理 1776年 ワット ワット式蒸気機関発明 電気 1800年 ボルタ 異種金属電池の発明 電気 1822年 バベッジ コンピュータ原型を試作 生物 1859年 ダーウィン、ウォーレス 進化の自然選択説提唱 電気 1864年 マックスウェル 電磁場の方程式 生物 1865年 メンデル 遺伝の法則 化学 1869年 メンデレーフ 元素の周期律の発表 電気 1876年 ベル 電話の発明 化学 1879年 イーストマン
写真用フィルム乾板を発明 電気 1880年 エジソン 発電機の発明 原子 1895年 レントゲン X線の発見 原子 1896年 ベクレル ウランの放射線を発見 原子 1897年 ウィルソン 霧箱の発明 原子 1898年 キュリー夫妻 ラジウム及びポロニウムの発見 物理 1903年 ライト兄弟 人類初の動力飛行に成功 化学 1908年 ハーバー アンモニア合成を確立 物理 1916年 アインシュタイン 一般相対性理論提唱 生物 1921年 フレミング リゾチームの発見 生物 1928年 フレミング ペニシリンの発見 化学 1935年 カローザス ナイロンの発明 原子 1938年 ハーン 原子核分裂の発見 原子 1942年 フェルミ 原子核分裂の連鎖反応制御に成功 原子 1952年 福井謙一 フロンティア電子理論の提唱 電子1956年 ブラッテン トランジスタの発明 ホーム アルケミストの小部屋 に戻る |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||