| 懸偪峴楍栤戣傪峫偊偰傒傞 偙偺儁乕僕偱偼丄媄弍巑堦師帋尡偱弌戣偝傟偨懸偪峴楍栤戣傪丄侾丏弌戣偝傟偨曽朄偵廬偭偰夝偔丄俀丏僔儈儏儗乕僔儑儞傪梡偄偰摼偔丄偺俀捠傝偺夝朄傪帵偟偰偄傑偡丅 摉慠偺偙偲側偑傜丄侾丏偺曽朄偱偼丄愝栤偑媮傔傞摎偊偑摼傜傟傑偡丅偦偟偰丄偦偺夝偒曽偑堦斒揑側曽朄偱偁傞偙偲偼丄壓偵帵偡傛偆偵丄懠偺倂倕倐僒僀僩偱傕妋擣偟偰偄傑偡丅 俀丏偺曽朄偱偼丄懸偪峴楍偺尨棟偵婎偯偒丄俤倶們倕倢偺倁俛俙乮僾儘僌儔儈儞僌婡擻乯偵傛傝懸偪峴楍偺敪惗傪僔儈儏儗乕僔儑儞偟丄摎偊傪摼傛偆偲偟傑偟偨丅 寢壥偼丄侾丏偲俀丏偱堎側傞暯嬒懳墳帪娫偲側偭偰偟傑偄傑偟偨丅偦偺尨場偵偮偄偰丄峫偊偰偄傞偲偙傠偱偡丅偙偙偵栤戣偑偁傞偲偺偛巜揈偑捀偗傞偲岾偄偱偡丅偳偙偐偵彫偝側娫堘偄偑偁傞偲偼巚偆偺偱偡偑丄偦傟傪帺暘帺恎偱尒偮偗傞偙偲偼擄偟偄巕倲倫偱偡丅 媄弍巑堦師帋尡丂婎慴壢栚偱弌戣偝傟偨栤戣暥 懸偪峴楍栤戣偼僆儁儗乕僔儑儞僘丒儕僒乕僠乮俷俼乯偺戙昞揑側栤戣偱丄偦偺庤朄偼峀偔棙梡偝傟偰偄傑偡丅嬧峴偺憢岥偲懸偪帪娫丄昦堾偱偺懸偪帪娫側偳偑偦偺揟宆椺偱偟傚偆丅 偝偰丄媄弍巑堦師帋尡丒婎慴壢栚偱偼偙偺懸偪峴楍偵娭偡傞栤戣偑夁嫀偵俁夞弌戣偝傟偰偄傑偡丅暯惉俀俈擭嘥亅侾亅俀乮暯惉俀俁擭嘥亅侾亅俀偲摨偠栤戣乯偲暯惉俀俆擭嘥亅侾亅俆偱丄慡栤摨偠曽朄偱夝偗傑偡丅 弌戣偝傟偨栤戣傪帵偟傑偡丅 暯惉俀俈擭丂嘥亅侾亅俀  暯惉俀俆擭丂嘥亅侾亅俆  侾丏栤戣暥偵増偭偨夝朄 偳偪傜傕摨偠栤戣偱偁傞偙偲偑暘偐傝傑偡丅嬧峴俙俿俵偱偁傞偐丄墂偺夵嶥偱偁傞偐偺堘偄掱搙偱偟傚偆丅 忋偺栤戣丄嬧峴偺俙俿俵丄偺夝偒曽偵偮偄偰彮偟峫偊偰傒傑偡丅  俙俿俵偱偺暯嬒張棟帪娫偼侾恖摉偨傝俁侽昩偲帵偝傟偰偄傑偡丅愒巐妏偱乽張棟偵梫偡傞帪娫偼巜悢暘晍偵偟偨偑偆乿傪埻偄傑偟偨偑丄偙偺栤戣偱偼丄張棟偵梫偡傞帪娫偼暘晍側偟偺俁侽昩偱偡丅俙俿俵偺埖偄偑傢偐傜偢偵帪娫偑偐偐傞恖丄僷僗儚乕僪傪擖傟娫堘偊偰嵞擖椡偡傞恖丄偄偔傜堷偒弌偦偆偐偲偦偺応偱峫偊傞恖側偳丄彅乆偺忦審偺寢壥偲偟偰偺巜悢暘晍偼壛枴偝傟偰偄傑偣傫丅寁嶼偑暋嶨偵側傝丄梌偊傜傟偨抁偄帪娫偱偼夝摎晄擻偵娮傞偲偄偆偺偑偦偺棟桼偱偟傚偆丅 暯嬒張棟帪娫偼俁侽昩丄扨埵帪娫摉偨傝乮侾帪娫摉偨傝乯偺張棟恖悢偼侾俀侽恖偲側傝傑偡丅 媄弍巑堦師帋尡丒婎慴栤戣丂暯惉侾俇擭乣俀俉擭偺夝摎廤偺拞偺俙侾俇乮懸偪峴楍乯偱偼夝摎師偺傛偆偵側偭偰偄傑偡丅 乮堷梡乯 H27擭丂嘥亅侾亅俀丂偲丂H23擭丂嘥亅侾亅俀 乮愒帤偼偙偺栤戣偑娙扨側栤戣乮僒乕價僗栤戣乯偱偁傞偙偲傪帵偟偰偄傞乯 僆儁儗乕僔儑儞僘丒儕僒乕僠偵娭偡傞揟宆揑側栤戣偱偁傞丅 悢幃偵抣傪戙擖偡傟偽傛偄偩偗偱偁傞偺偱丄懠偺僆儁儗乕僔儑儞僘丒儕僒乕僠偲偼暿偺暘椶偲偟偰偄傞丅 H俀俈擭丂嘥乕侾亅俀 H俀俈擭搙栤戣丂 惓摎丗丂嘋丂 乮夝摎乯 扨埵帪娫傪侾帪娫偲偡傞丅 扨埵帪娫偁偨傝偺暯嬒摓拝恖悢俙亖俆侽恖 扨埵帪娫偁偨傝偺暯嬒張棟恖悢俛亖侾俀侽恖乮俁俇侽侽乛俁侽乯 棙梡棪俠=俙乛俛亖俆侽乛侾俀侽亖侽丏係侾俈 懸偪峴楍挿俢亖俠亐乮侾亅俠乯亖侽丏俈侾俆 暯嬒懸偪帪娫俤亖俢亊暯嬒張棟帪娫乮俁侽昩乯亖俀侾昩 暯嬒懳墳帪娫亖俤亄暯嬒張棟帪娫乮俁侽昩乯亖俆侾昩 慺捈偵愝栤偺悢帤傪曄悢偵戙擖偟偰偄偗偽摎偊偵帄傝傑偡丅 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮堷梡廔傢傝乯 偙偺栤戣傪夝偔億僀儞僩偼係偮偁傞幃偺娫偺娭學乮峔憿乯傪棟夝偡傞偙偲偱偡丅忋偱栤戣暥偵愒慄傪擖傟偰帵偟偨傛偆偵丄彮偟偩偗擖傝慻傫偱偄傑偡丅栤戣暥偺僆儕僕僫儖傪帵偟丄偦偺娭學傪惍棟偟側偍偡偲師偺傛偆偵側傝傑偡丅張棟偡傞弴斣偑棟夝偱偒傟偽偙偺栤戣偼娙扨偵夝偗傑偡丅偦傫側暋嶨偵峫偊側偔偰傕丄暘偐偭偨悢抣傪戙擖偟偰偄偒丄嵍曈偵悢帤偑尰傟傟偽丄師偺幃傊偲恑傫偱偄偔丅偙偺峴偒摉偨傝偽偭偨傝朄偱傕偙偺栤戣偼娙扨偵夝偗傞偲巚偄傑偡丅 乮栤戣暥乯 懸偪峴楍丂亖丂棙梡棪丂亐丂乮侾亅棙梡棪乯 暯嬒懸偪帪娫丂亖丂懸偪峴楍挿丂亊丂暯嬒張棟帪娫 棙梡棪丂亖丂扨埵帪娫摉偨傝偺暯嬒摓拝恖悢丂亐丂扨埵帪娫摉偨傝偺暯嬒張棟恖悢 暯嬒懳墳帪娫丂亖丂暯嬒懸偪帪娫丂亄丂暯嬒張棟帪娫 乮夝摎乯 愒帤偼栤戣暥傛傝偡偱偵梌偊傜傟偰偄傞傕偺 棙梡棪丂亖丂扨埵帪娫摉偨傝偺暯嬒摓拝恖悢丂亐丂扨埵帪娫摉偨傝偺暯嬒張棟恖悢 懸偪峴楍丂亖丂棙梡棪丂亐丂乮侾亅棙梡棪乯 暯嬒懸偪帪娫丂亖丂懸偪峴楍挿丂亊丂暯嬒張棟帪娫 暯嬒懳墳帪娫丂亖丂暯嬒懸偪帪娫丂亄丂暯嬒張棟帪娫 幃傪暲傋懼偊傞偲丄側傫側偔偙偺栤戣偑夝偗傞偙偲偑暘偐傝傑偡丅
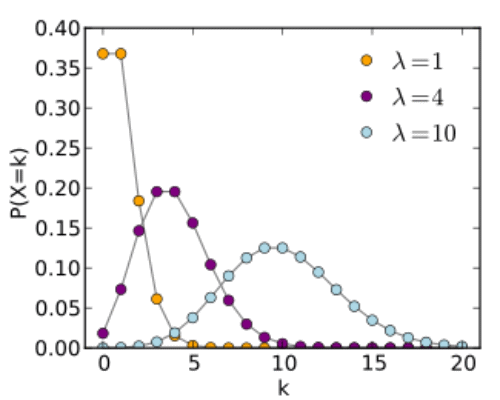
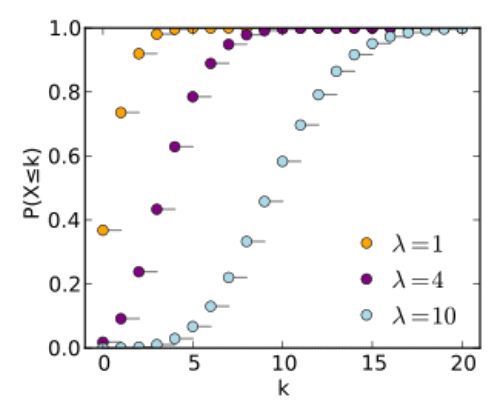
俀丏僔儈儏儗乕僔儑儞偵傛傞夝朄 億傾僜儞暘晍偲巜悢暘晍娭悢 億儚僜儞暘晍乮倂倝倠倝倫倕倓倝倎乯 掕悢兩亜侽偵懳偟丄帺慠悢傪抣偵偲傞妋棪曄悢倃偑 丂丂俹乮倃亖倠乯亖兩倠倕倶倫乮亅兩乯乛倠両 傪枮偨偡偲偒丄妋棪曄悢倃偼僷儔儊乕僞兩偺億傾僜儞暘晍偵廬偆偲偄偆丅 乮拲庍傪壛偊傞乯 兩偼扨埵帪娫拞偵帠徾偑敪惗偡傞暯嬒夞悢 倫乮倶亖倠乯偼扨埵帪娫拞偵帠徾偑倠夞敪惗偡傞妋棪枾搙
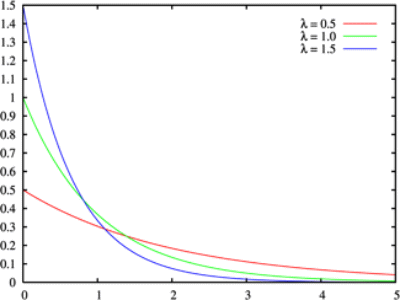
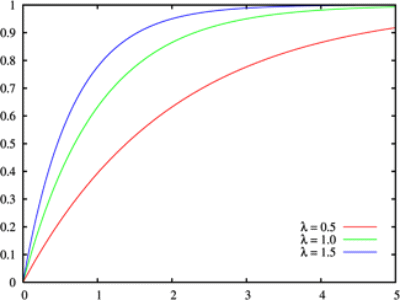
巜悢暘晍乮倂倝倠倝倫倕倓倝倎乯 巜悢暘晍偼丄惓偺僷儔儊乕僞兩偵懳偟偰妋棪枾搙娭悢偑丄 丂丂倖乮倶丟兩乯亖兩倕倶倫乮亅兩倶乯丂乮倶亞侽乯丄丂亖侽丂乮兩亙侽乯 偱梌偊傜傟傞暘晍偱偁傞丅偙偺偲偒丄椵愊暘晍娭悢偼 丂丂俥乮倶丟兩乯亖侾亅倕倶倫乮亅兩倶乯丂乮倶亞侽乯丄丂亖侽丂乮兩亙侽乯 乮拲庍傪壛偊傞乯 兩偼扨埵帪娫拞偵帠徾偑敪惗偡傞暯嬒夞悢 倖乮倶丟兩乯偼帠徾偺敪惗娫妘偑倶扨埵帪娫偱偁傞妋棪枾搙
傕偆彮偟暘偐傝堈偔彂偔偲丄 扨埵帪娫偁偨傝暯嬒兩夞婲偙傞儔儞僟儉側僀儀儞僩偵懳偟偰丄 乮侾乯扨埵帪娫偵帠徾偑婲偒傞夞悢偼暯嬒兩偺億傾僜儞暘晍偵廬偄 乮俀乯帠徾敪惗娫妘偼暯嬒侾乛兩偺巜悢暘晍偵廬偆丅 埲忋偺偙偲傪摜傑偊丄偝傜偵丄惉彂乽俤倶們倕倢偵傛傞俷俼墘廗乮摗揷彑峃丄擔壢媄楢丄俀侽侽俀擭乯偺夝朄偵廬偭偰夝偄偰偄偔丅 俆丏俀丂懸偪峴楍僔儈儏儗乕僔儑儞丂乮倫丏侾俀侽乯 媞偑侾帪娫乮俇侽暘乯摉偨傝俁侽戜摓拝偡傞偲壖掕偟傑偡丅偮傑傝丄暯嬒摓拝棪兩亖俁侽乛俇侽亖侽丏俆恖/暘 暯嬒摓拝娫妘丂侾乛兩亖俀暘乛恖 摓拝偺暘晍偲摓拝娫妘偼丄媞偑侾暘娫偵暯嬒俀恖丄儔儞僟儉偵摓拝偡傞偲壖掕偟偨偺偱丄摓拝帪娫偺娫妘偼暯嬒乮侾乛兩乯亖俀暘偺巜悢暘晍偵廬偄傑偡丅幃偱彂偔偲丄 丂丂丂倷丂亖丂倕倶倫乮亅兩倴乯 偲側傝傑偡丅偙偙偱 倴 偼媞偺摓拝帪娫娫妘丄 倷 偼偦偺帪娫娫妘偵拝偔妋棪偱偡丅倷 偼妋棪偱偡偐傜丄侽偐傜侾偺娫偺悢抣偲側傝傑偡丅 丂丂丂倴丂亖丂亅侾乛兩亊倢値乮倷乯丂亖丂亅俀倢値乮倷乯 偙偺 倷 偵侽偐傜侾偺棎悢傪戙擖偡傟偽丄摓拝帪娫娫妘偺棎悢 倴 偑寁嶼偱偒傑偡丅 埲忋偺偙偲傪摜傑偊傞偲丄忋偺栤戣偱媞偺俙俿俵傊偺摓拝帪娫偺娫妘 偼暯嬒 侾乛兩 偺巜悢暘晍偵廬偄丄幃偱彂偔偲丄 丂丂丂倷丂亖丂倕倶倫乮亅兩倴乯丂丂丂丂偨偩偟丄倴 偼媞偺摓拝帪娫娫妘丄倷 偼偦偺帪娫娫妘偵摓拝偡傞妋棪偱偡丅 僾儘僌儔儉傪慻傫偱弴師寁嶼傪偡偡傔傑偡丅
俆侽恖栚傑偱偺寁嶼偼塃昞偺傛偆偵側傝傑偡丅 侾恖栚偼俙俿俵偑奐偄偰偐傜俀昩屻偵摓拝偟傑偡偑丄張棟偵俁侽昩偐偐傞偺偱丄偙偺侾恖栚偑俙俿俵偐傜弌偰偄偔偺偼俙俿俵偑奐偄偰偐傜俁俀昩屻偲側傝傑偡丅 俀恖栚偼侾侾昩屻偵摓拝偟丄偡偖偵俙俿俵偱偺張棟傪偼偠傔傜傟傟偽椙偄偺偱偡偑丄侾恖栚偑傑偩張棟拞偱偡偺偱丄寢嬊俁俀昩偐傜張棟傪巒傔偰俇俀昩偵偦偺張棟偑廔傢傞偙偲偵側傝傑偡丅 偙偺梫椞偱俆侽恖栚傑偱張棟傪懕偗傑偡丅俆侽恖栚偺摓拝帪娫偼俁俈侽係昩偱栺侾帪娫乮俁俇侽侽昩乯偑宱夁偟偰偄傞偙偲偑暘偐傝傑偡丅 俙俿俵偱偺張棟帪娫傪娷傔偨懸偪帪娫偼丄張棟偵偐偐傞帪娫乮廔椆乮昩乯乯偐傜摓拝帪娫乮昩乯傪堷偄偨帪娫偲側傝丄壓偺昞偱偼俆侽恖偺暯嬒偑係侾丏俁昩偲側傝傑偡丅 侾侽侽侽侽恖偑偙偺俙俿俵傪巊梡偡傞応崌偺僩儔僀傾儖寁嶼傪俆夞峴偄傑偟偨丅 俆侽恖偱栺侾帪娫偱偡偐傜丄侾侽侽侽侽恖偱偼栺俀侽帪娫暘偺寁嶼偱偡丅恖悢偑彮側偄帪偵偼摼傜傟傞岆嵎偑戝偒偔側傝傑偡偑丄侾侽侽侽侽恖偺寁嶼偲傕側傝傑偡偲丄摼傜傟傞抣偼偁傞掱搙廂澥偟偰偒傑偡丅 壓偺昞偼俆夞偺僩儔僀傾儖偺寢壥偱偡丅 傑偢丄張棟恖悢偱偡偑丄侾帪娫摉偨傝俆侽丏侽恖偱偡丅摓拝偐傜俙俿俵偱偺張棟偑廔椆偡傞傑偱偺帪娫偼暯嬒偱係侽丏俁昩偲媮傑傝傑偟偨丅
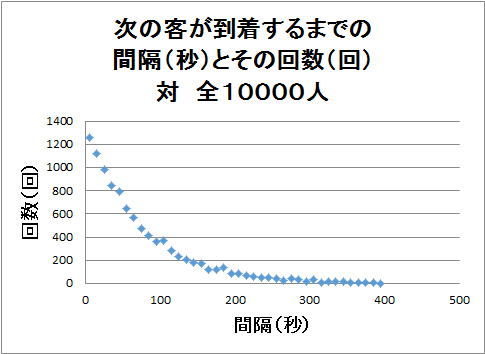 俁丏巆傞栤戣 俀丏偺栤戣暥偵増偭偨夝朄偱偼丄俆侾昩偲偄偆摎偊偑摼傜傟丄偙傟偼擔杮媄弍巑夛偑帵偟偰偄傞惓摎偲傕堦抳偟偰偄傞丅 堦曽丄俀丏偺僔儈儏儗乕僔儑儞偵傛傞夝朄偱摼傜傟傞俙俿俵摓拝偐傜偦偺張棟偑廔傢傞傑偱偺帪娫偼栺係侽昩偲側傝丄摎偊偑堎側偭偨丅 僔儈儏儗乕僔儑儞偱惓摎偑摼傜傟偰偄側偄偙偲傪慜採偵丄偙偺摼傜傟偨寢壥偺嵎偑偳偙偵偁傞偐丄偦偺壜擻惈傪尒偰偄偔偲丄 崱夞僔儈儏儗乕僔儑儞偵梡偄偨幃偼丄 丂丂丂倷丂亖丂倕倶倫乮亅兩倴乯 偱偁傞偺偵懳偟丄巜悢暘晍偱梌偊傜傟偰偄傞幃偼丄 丂丂倖乮倶丟兩乯亖兩倕倶倫乮亅兩倶乯丂乮倶亞侽乯丄丂亖侽丂乮兩亙侽乯 偱偁傞丅 偙偺巜悢崁偵兩偑偐偐偭偰偄傞偐偄側偄偐偺嵎偱偁傞丅 兩傪妡偗偨幃偱僔儈儏儗乕僔儑儞傪帋傒偨偑丄侾帪娫摉偨傝偺摓拝恖悢偑慜採乮侾帪娫摉偨傝俆侽恖乯偐傜曄摦偟偰偟傑偄丄巚偆傛偆側寢壥偲偼側偭偰偄側偄丅 係丏尰嵼偺寢榑 栤戣偼栤戣偲偟偰擣幆偟丄僔儈儏儗乕僔儑儞曽朄偑尒偄偩偣傞傑偱偼偟偽傜偔偼壗傕偣偢偵丄偙偺傑傑偲偟偰偍偔丅 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂媄弍巑堦師帋尡丒婎慴壢栚丂暯惉侾俇擭乣俀俉擭俁俆俇栤戣夝摎廤偵栠傞 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||