| 平成28年度 技術士一次試験 基礎科目 解答 10月18日に発表された本年の試験問題の解答を作成する。 技術士一次試験の目次一覧に戻る 書籍 技術士一次試験 基礎科目を極める(2022年版) 平成16年度~令和3年度 基礎科目の解答を収録 日本技術士会のホームページより 技術士第一次試験 基礎科目の問題 基礎科目について、 過去の問題と今回の問題比較 類似の問題が多数ありますので、やはり過去問をしっかりとやるということに尽きます。 過去問をやっていれば解ける問題、および簡単な問題は問題番号を赤字としました。 各群より3問選択 合計で15問解答 内8問正解で基礎科目は合格 過去問関連の出題は、1群はズバリが2問、類似が3問 2群はズバリが2問、類似が4問 3群はズバリが3問、類似はなし 4群はズバリが3問、類似はなし 5群はズバリが2問、類似が1問 なお、日本技術士会が現在公開している平成16年~28年の過去問356題の解答は 技術士一次試験・基礎科目 H16年~28年の356全問解答集 にまとめて記しています。 簡単に解けるボーナス問題は問題番号を赤字で示す。 1群 Ⅰ-1-1 信頼度 少し複雑にしてはあるが、過去問はH27-1-1-1、H16-1-1-4、H24-1-1-1、H23-1-1-1、H22-1-1-3、H19-1-1-1、H18-1-1-1、H17-1-1-1(違うように見えるが同じ)、H17-1-1-6、H16-1-1-3 Ⅰ-1-2 抜き取り検査 H26-1-1-3と同じ Ⅰ-1-3 プラスチック定規の強度 H25-1-1-2と同じ Ⅰ-1-4 PERT法 H25-1-1-4、H23-1-1-3と基本的に同じ。少し複雑にしてあるが・・・ Ⅰ-1-5 生産個数最適化 H24-1-1-5と基本的に同じ Ⅰ-1-6 エンジニアリングデザイン 新規問題であるが、難しくはない。 2群 Ⅰ-2-1 天気の確率 H24-1-2-3、H16-1-2-3に同じ Ⅰ-2-2 真理値表の演算 H25-1-2-3、H23-1-2-3に類似 ただし、同じではない Ⅰ-2-3 アルゴリズム H26-1-2-2、H24-1-2-5に類似 ただし、同じではない Ⅰ-2-4 アクセス時間 H23-1-2-4にほぼ同じ Ⅰ-2-5 ネットでデータ送信 H19-1-2-2と同じ Ⅰ-2-6 表現できるアドレス数 H23-1-2-1に類似 2進数の問題 3群 Ⅰ-3-1 定積分の近似式 H18-1-3-2に同じ Ⅰ-3-2 ヤコビアン 新規問題 Ⅰ-3-3 単位ベクトル H22-1-3-3に同じ Ⅰ-3-4 重積分値を求める 新規問題 Ⅰ-3-5 固有振動数の大小 H23-1-3-4と同じ、H25-1-3-2に類似 Ⅰ-3-6 引っ張り応力の比 新規問題 基本問題ではあるが・・・ 4群 Ⅰ-4-1 アンモニア合成反応 H25-1-4-1と同じ Ⅰ-4-2 元素の中性子、電子の数、同位体、同素体 新規問題 多少関係があるものはH17-1-4-2 Ⅰ-4-3 金属の性質 H22-1-4-3と同じ Ⅰ-4-4 材料の力学特性試験 新規問題 Ⅰ-4-5 コドンとタンパク質 新規問題 Ⅰ-4-6 DNAの変性 H24-1-4-5と同じ 5群 Ⅰ-5-1 産業廃棄物の処理の流れ 新規問題 Ⅰ-5-2 生物多様性の保全 H22-1-5-3と同じ Ⅰ-5-3 電気エネルギーの貯蔵や発電 新規問題 Ⅰ-5-4 エネルギー基本計画 新規問題 Ⅰ-5-5 科学技術コミュニケーション H25-1-5-5と同じ Ⅰ-5-6 科学史・技術史上の人物と業績 類似問題は、H27-1-5-6、H26-1-5-6、H25-1-5-6、H23-1-5-5、H22-1-5-5、H21-1-5-5 解答 1群 設計・計画に関するもの Ⅰ-1-1 信頼度 解答:④ 故障率は1-x、並列の場合は2つの回路が同時に故障すると初めて故障となるから、並列回路の故障率は(1-x)^2 従って、並列回路の信頼度は(1-故障率)=(1-(1-x)^2)となる。 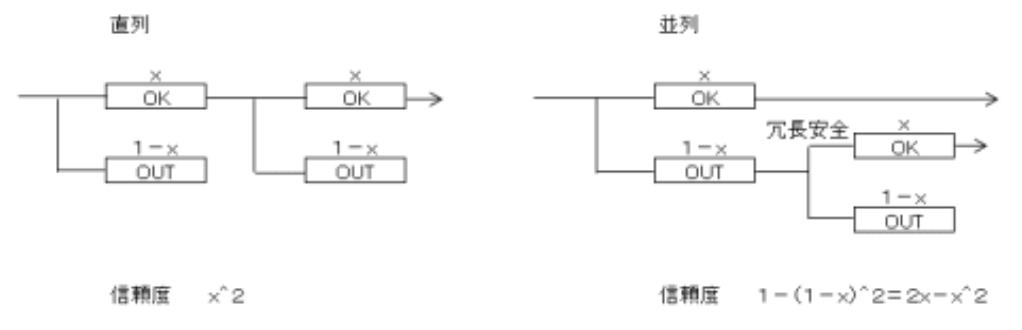 これをもとに、問題を数式化すると、 0.90×(1-(1-x)2)×0.90=x×0.95×x この式より、x=0.92 この値を上式に代入すると、左辺、右辺共に0.804となる。 Ⅰ-1-2 抜取検査 解答:④ 答えの通り Ⅰ-1-3 プラスチック定規の強度 解答:④ 答えの通り Ⅰ-1-4 PERT法 解答:④ 複雑な工程と日数が示されているが、各ルートの必要日数を頭から積み上げていけば答えに到達できる。たとえば中央にあるポイント⑥では、ルートp-b1では25日必要であるが、p-a1-a2-ダミーでは33日と長くかかる。従って、ルートp-b1の工程は余裕を持っていることがわかる。縮めるとすれば、工程p-a1-a2-ダミーのどこかである。同じように日数の積み上げを行って行けば、どこに縮めしろがあるかがわかる。 なお、ダミーとは、工程a2が終了してポイント③に到達しないとポイント⑥からの工程b2が開始できないことを示す記号である。 下の図に示すように、作業の進行順に必要日数を求めていくと、○で囲んだルートがクリティカルパスとなる。 費用を支払って工期を1日短くするとすると、a2かb3であるが、b3の方が追加費用が安い。 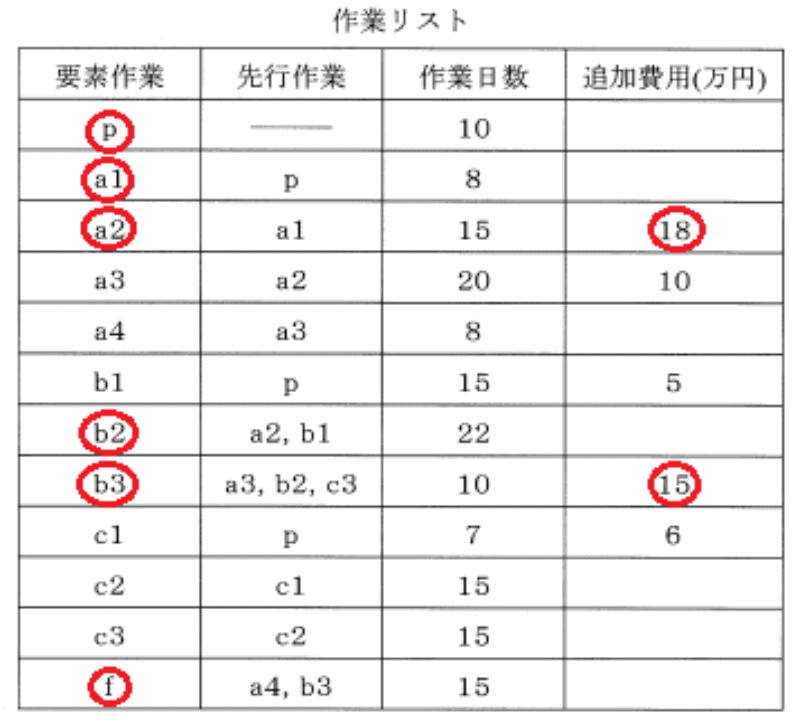  Ⅰ-1-5 生産個数最適化 解答:⑤ 不等式を立ててグラフを描くとP1が3個、P2が3個、が答えになるのがわかる。 製品P1の数をx、P2の数をyとすると、x≦5、x+2y≦9、2y≦6.  しかし、解答時間からは直接数字を入れてみる方が早い。利益の”-”は条件が満たされていないことを意味している。
Ⅰ-1-6 エンジニアリングデザイン 解答:① 新規問題であるが、難しくはない。 問題と解答を読み合わせ理解する。 2群 情報・論理に関するもの Ⅰ-2-1 天気の確率 解答:④ 解答①~⑤に関して考え方はすべて同じであるので、正解の④の場合の確率表を作る。
従って、2日後が晴れである確率は、1/8+1/8+1/16=5/16となり、④は不適切である。 Ⅰ-2-2 真理値表の演算 解答:② 下表より②が正解であることがわかる。 A and B(A・B)はAとBがともに1なら1、それ以外は0 A or B(A+B)はAかBのどちらかが1ならば1、それ以外は0
Ⅰ-2-3 アルゴリズム 正解:① (ア) N>0の時は繰り返し計算 (イ) N=0になった時に計算ルーチンより抜ける (ウ) Nに商を入れる 問題文の 11÷2=5 余り1 5÷2=2 余り1 の数字5の話である。 Ⅰ-2-4 アクセス時間 解答:④ コンピュータは一度使ったデータは複数回利用される可能性があるのでキャッシュに登録する。キャッシュはアクセス時間が短いのでコンピュータの処理速度を向上させることができる。だが、キャッシュは主記憶に比べて容量が大きくないという弱みがある。 あるデータが来た時に、コンピュータはまずキャッシュを見に行く。そこにデータがない場合に主記憶を見に行く。 アクセス時間の計算式は、1.00×0.95+100×0.05=5.95ns Ⅰ-2-5 ネットでデータ送信 解答:④ 問題文の通りである。付加ビット(パリティビット)は正答④ではたとえば次のようになり、同時に2ビットが反転すればその誤りを検出できない。パリティビットに赤色を付けた。 10101001 → 10000001 Ⅰ-2-6 表現できるアドレス数 解答:⑤ 題意より、(216)8/(28)4=296である。 3群 解析に関するもの Ⅰ-3-1 定積分の近似式 解答:③ この問題の意味をイメージでとらえる。 問題の意味は、x軸とf(x)で囲まれた、x=-1からx=1までの面積を積分で求めるというものである。 ① f(-1)とf(1)の中間点f(0)を妥協高さとして、長方形の面積を求めている。 ② f(-1)とf(1)を頂点とする台形の面積を求めている。 ③ ???? ④ (①+②)/2である。 ⑤ ①×1/3+④×2/3である。 以上、説明を加えたが、一番端的なのは、それぞれのf(x)の係数を足した数字が、③のみ2とならないことである。 ①2 ②1+1=2 ③1/4+1+1/4=3/2 ④1/2+1+1/2=2 ⑤1/3+4/3+1/3=2 Ⅰ-3-2 ヤコビアン 解答:③ この問題は試験会場でいくら考えても答えが出てこない。知っているかどうかである。 二重積分のヤコビアン  (1.6.6)式のヤコビアンを解くと答えが得られる。 x=u+v、y=uvであるから、∂x/∂u=1、∂x/∂v=1、∂y/∂u=v、∂y/∂v=u 従って、J(u,v)=u-v となる。 Ⅰ-3-3 単位ベクトル 解答:② なじみが薄いギリシャ文字なのでξ(クシー)→α、η(エータ)→βと書き直す。 題意より、α、βの関数N1、N2、N3、N4は、 N1=1/4(1-α)(1-β) N2=1/4(1+α)(1-β) N1=1/4(1+α)(1+β) N1=1/4(1-α)(1+β) [N1,N2,N3,N4]=a0+αa1+βa2+αβa3 a0、a1、a2、a3は定数項からなる行ベクトル a0=1/4[1,1,1,1] 1/4を省略して表を作る。
従って、②が答えとなる。 確認計算をする。1/4を省略すると、 [N1,N2,N3,N4]=[1-α-β+αβ,1+α-β-αβ,1+α+β+αβ,1-α+β-αβ] =a0+αa1+βa2+αβa3=[1,1,1,1]+α[-1,1,1,-1]+β[-1,-1,1,1]+αβ[1,-1,1,-1] =[1,1,1,1]+[-α,α,α,-α]+[-β,-β,β,β]+[αβ,-αβ,αβ,-αβ] さらにダメ押し確認する。 =[1-α-β+αβ,1+α-β-αβ,1+α+β+αβ,1-α+β-αβ] Ⅰ-3-4 重積分値を求める 解答:⑤ 難しそうに見えるが、実は簡単である。 まず内側の積分を実施し、続いて外側の積分を実施する。 内側の積分 ∫(x+y)dx=[1/2×x2+xy]x=0 to (2-y)=-y2/2+2 外側の積分 ∫(-y2/2+2)dy=[-y3/6+2y]y=0 to 2=8/3 Ⅰ-3-5 固有振動数の大小 解答:① 感覚に訴える問題である。 ピーンと張られたはり(c)は固有振動数が大きく、逆に片方が固定されていないはり(b)は固有振動数が小さい。 Ⅰー3-6 引っ張り応力の比 解答:④ ヤング率の定義から考えるとすぐに解ける問題である。 σ=F/A=E(ΔL/L) 但し、力Fが断面積Aにかかる。 棒Aおよび棒Bの添字をほどこし、両者で(ΔL/L)が等しいことを考慮すれば、解答が得られる。 σa/Ea=σb/Eb 従って、σa/σb=Ea/Eb 4群 材料・化学・バイオに関するもの Ⅰ-4-1 アンモニア合成反応 解答:④ ルシャトリエの法則である。 ルシャトリエの原理(Wikipedia)ではアンモニアを例に、議論が展開されている。 Ⅰ-4-2 元素の中性子、電子の数、同位体、同素体 解答:④ 元素記号の左横に2つの数字が並ぶが、下が原子番号、上が質量数である。 原子番号は陽子の数、質量数は陽子+中性子の数、そして原子が中性である(荷電していない)ならば電子の数=陽子の数である。 ① 40-20≠40-18 ② 35-17≠37-17 ③ 全くの無関係 ④ 電子の数=陽子の数=原子番号 従って、17=17は正しい。 ⑤ これを同位体という。同素体とは、たとえば炭素でいうと、グラファイト、ダイヤモンド、フラーレンの関係。 Ⅰ-4-3 金属の性質 解答:③ 知っているかどうかの問題。 直感的にはアルミニウムは軽い(比重2.7)。従って(ア)か(イ)。 銅は電気を良く通す。これは電気抵抗が小さいということ。銅線に変えてアルミニウム線を用いたら、などという話もある。銅よりは電気が通りにくいが軽いということ。従って、(ウ)か(オ)。 融点はアルミニウムが低いことは知っての通り。銅文明が鉄文明よりも先に起こったのは、周知の通り。従って(ア)。 全てを満足する答えは③。
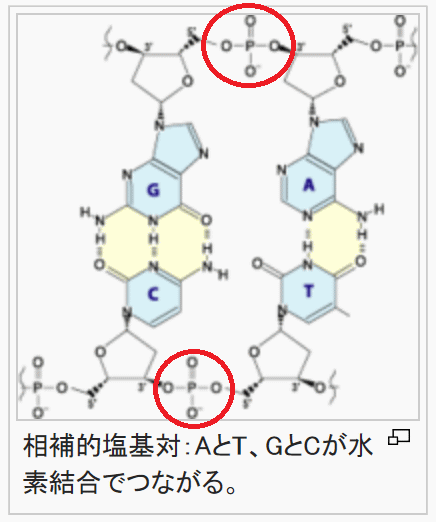
電気を通しやすい金属は熱も通しやすい。 (参考) 電気の流れは、金属イオン格子の中を伝導電子が移動することで生じている。熱も同様に伝達されているようだ。 金属の電気抵抗率(20℃)と熱伝導率(300K)はWikipediaに金属名を入れると調べることができる。 電気抵抗率(Wikipedia)には次の記述がある。 単位は、オームメートル(Ω・m)である。慣例的に Ω・cm もよく使われる。自由電子の数密度が大きく影響する。自由電子の数が多ければ多いほど電気抵抗率は低くなり。少なければ少ないほど電気抵抗率は高くなる。自由電子の数が限りなく0であれば、それは絶縁体である。 電気抵抗率の逆数を電気伝導率(導電率)と呼ぶ。 下表は、電気と熱を通しやすい金属から順に並べている。電気抵抗率の単位はnΩ・mで、電気伝導率の単位はその反対の1/(nΩ・m)となる。電気伝導率と熱伝導率の関係をグラフ化すると、きれいな直線関係となった。 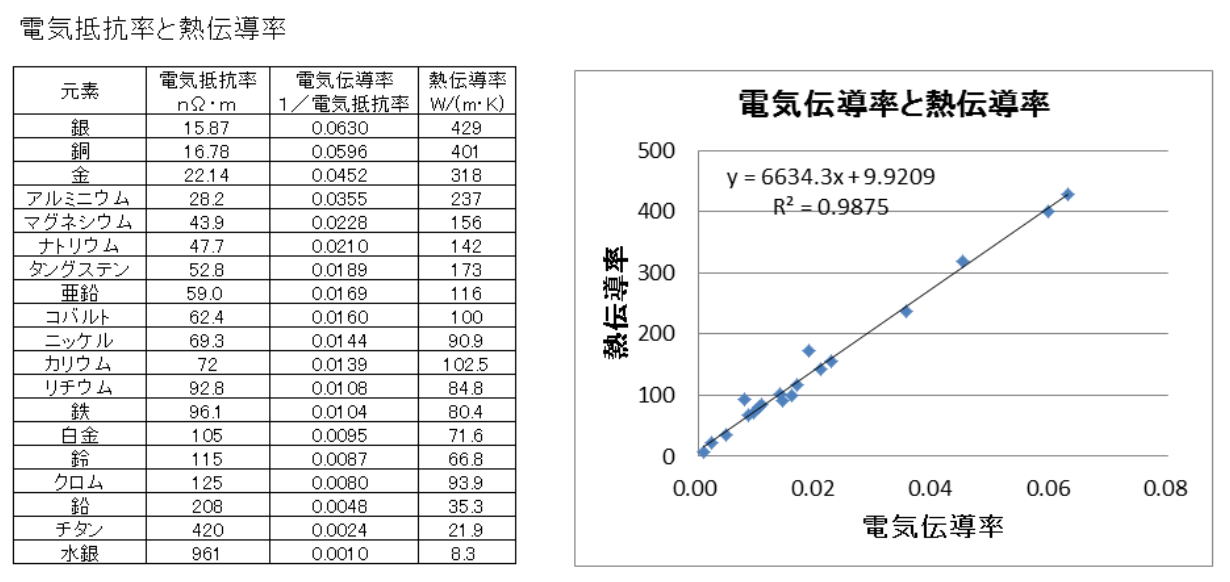 Ⅰ-4-4 材料の力学特性試験 解答② 問題文および解答の通り。 Ⅰ-4-5 コドンとタンパク質 解答:① 問題文と解答の通り。 たとえば下図の左上では、UUUでもUUCでもフェニルアラニンが、UUAでもUUGでもロイシンが生成してくる。 なお、DNA鎖とRNA鎖では構成塩基が少し違っている(T→U)。 DNA(wikipedia)より DNA はデオキシリボース(五炭糖)とリン酸、塩基 から構成される核酸である。塩基はプリン塩基であるアデニン(A)とグアニン(G)、ピリミジン塩基であるシトシン(C)とチミン(T)の四種類ある。 RNA(Wikipedia)より RNAの核酸塩基はアデニン (A)、グアニン (G)、シトシン (C)、ウラシル (U) の4種で構成されている。アデニン、グアニン、シトシンは DNA にも同じ構造が見られるが、RNAではチミン (T) がウラシルに置き換わっており、相補的な塩基はアデニンとなる。チミンとウラシルは共にピリミジン環を持つ非常に似た塩基である。 コドン(Wikipedia)より 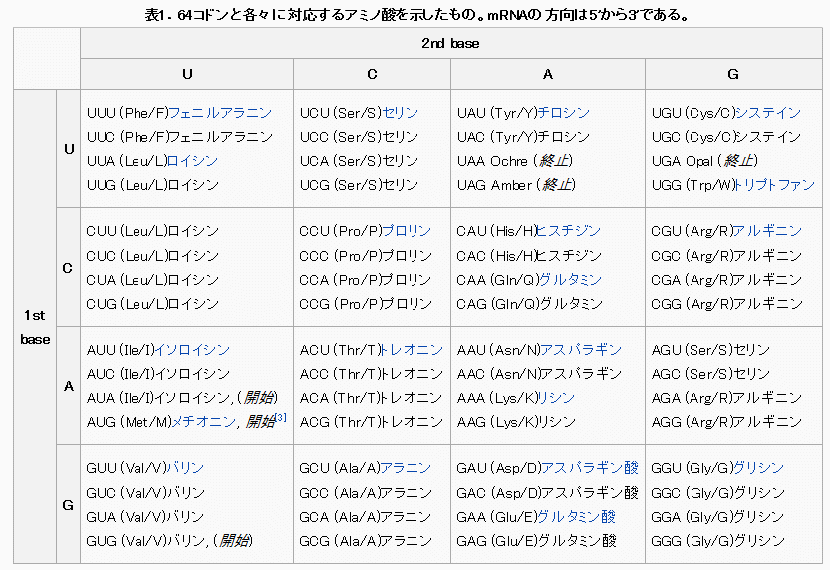 Ⅰ-4-6 DNAの変性 解答:③ GとCは三重結合(強い)、AとTは二重結合 赤丸で囲った部分がホスホジエステル結合。 図の上の部分がDNA二重鎖の一本、そして下の部分がDNA二重鎖のもう一本。 その2本のDNA鎖がG-C水素結合、あるいはA-T水素結合でつながり、DNAらせん構造を作り上げる。 DNA(Wikipedia)より
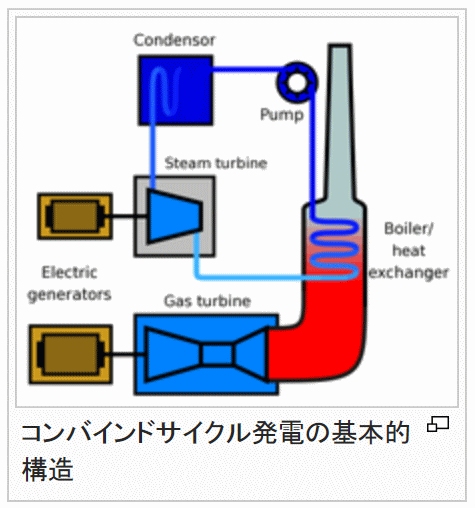
5群 環境・エネルギーに関するもの Ⅰ-5-1 産業廃棄物の処理の流れ 解答:⑤ 単純な計算問題である。 ① 83/207=40.1% ② 207/379=54.6% 207/13=15.9倍 ③ 124/83=1.49倍 ④ 159/379=42.0% ⑤ 379-83-290=6 6/379=1.6% 従って、⑤が誤り。引き算の答えが6であるところを60としたため。 Ⅰ-5-2 生物多様性の保全 解答:⑤ 問題文と解答の通り。 ⑤は琵琶湖の外来魚とかため池の外来亀、その他を計画的に駆除している。 外来種(Wikipedia) 生物多様性条約の第8条h項に「各々の締約国は、生態系、生息地、若しくは種を脅かす外来種の導入を阻止し、又はそのような外来種を制御し、若しくは撲滅すること」と明記されていることからもわかるように、生物多様性を脅かす外来種問題の解決は人間の、そして国の責務になっている。 特定外来生物による生態系等に係る被害の防止に関する法律(Wikipedia) 外来生物法(がいらいせいぶつほう)[1]、特定外来生物被害防止法(とくていがいらいせいぶつひがいぼうしほう)[2]と通称される。 日本在来の生物を捕食したり、これらと競合したりして、生態系を損ねたり、人の生命・身体、農林水産業に被害を与えたりする、あるいはそうするおそれのある外来生物による被害を防止するために、それらを「特定外来生物」等として指定し、その飼養、栽培、保管、運搬、輸入等について規制を行うとともに、必要に応じて国や自治体が野外等の外来生物の防除を行うことを定める。 Ⅰ-5-3 電気エネルギーの貯蔵や発電 解答:③ ③は蒸気タービンとガスタービンが逆である。 コンバインドサイクル発電(Wikipedia)
同じく「コンバインドサイクル発電」より、参考として、 石炭ガス化複合発電 (IGCC)燃料のガス化とコンバインドサイクル発電を組み合わせた発電形式を石炭ガス化複合発電 (IGCC) と呼ぶ。低質な石炭や重質油、廃棄物などは硫黄や塩素、重金属を含むことがあり、そのまま燃焼させて発電を行うとその環境負荷物質が大気中に排出されて問題となる。ガス化複合発電では、燃料をガス化したときにそれらの不純物を除去することができ、そうして生成したクリーンなガスを用いて発電を行うことで、環境負荷物質の少ない発電を行うことができる。また、従来の方式に比べて二酸化炭素排出量を削減することができ、石炭を燃料とした発電で石油発電並の二酸化炭素排出量を達成することができる。 科学コミュニケーションとはこのウェブサイトでは、「科学コミュニケーションとは、科学にかかわる情報を、科学者と科学者でない人たち(ここでは市民と呼びます)とがやりとりすること」としています。 1 科学コミュニケーションの3つの側面「科学コミュニケーション」とは、科学技術にたいする理解増進にとどまらず、より幅広いコミュニケーション活動を視野に入れたものです。
2 科学コミュニケーションにおける基本方針
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||